Version [58471]
Dies ist eine alte Version von TutoriumMathe3KlausurA erstellt von Jorina Lossau am 2015-08-29 12:52:32.
Tutorium Mathematik 3
| File | Last modified | Size |
|---|---|---|
| Mathe1.jpg | 2023-10-06 18:37 | 6Kb |
| Mathe3A11.pdf | 2023-10-06 18:37 | 53Kb |
| Mathe3A111.jpg | 2023-10-06 18:37 | 41Kb |
| Mathe3A112.jpg | 2023-10-06 18:37 | 43Kb |
| Mathe3A113.jpg | 2023-10-06 18:37 | 74Kb |
| Mathe3A114.jpg | 2023-10-06 18:37 | 51Kb |
| Mathe4.jpg | 2023-10-06 18:37 | 5Kb |
| Mathe5.jpg | 2023-10-06 18:37 | 3Kb |
| Mathe6.jpg | 2023-10-06 18:37 | 59Kb |
| Mathe7.jpg | 2023-10-06 18:37 | 19Kb |
Beispielklausur - Aufgaben
| 1. Aufgabe Berechnen Sie das zweifache Integral über das rechteckige Gebiet G mit  2. Aufgabe Gegeben ist die Funktion y (t) = e ^ 2t im Intervall [0; 0,5] 2.1 Berechnen Sie den integralen Mittelwert in diesem Intervall ! 2.2 Denken Sie sich diese Funktion periodisch mit T = 0,5 fortgesetzt und bestimmen Sie für diesen Fall den Effektivwert. 3. Aufgabe Man bestimme die allgemeine Lösung der Differentialgleichung mit Hilfe des λ -Ansatzes und einem geeigneten Ansatz für die partikuläre Lösung : y``+10y`+34y = sin(x) 4. Aufgabe Laplace-Transformation 4.1. Transformieren Sie unter Verwendung von Korrespondenztabellen folgende Funktionen vom Zeit- in den Bildbereich: a) f(t) = 4e^ -t b) f(t) = t*e^ -5t c) f(t) = 5cos (8t) 4.2. Transformieren Sie unter Verwendung von Korrespondenztabellen die Bildfunktionen in den Zeitbereich: 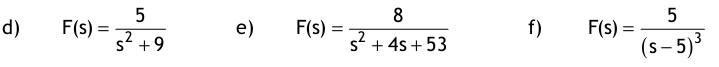 4.3. Lösen Sie die nachfolgende Anfangswertaufgabe mit Hilfe der Laplacetransformation :  5. Aufgabe Man löse die inhomogene Differentialgleichung mittels Variation der Konstanten: y`-2y = x* e^2x 6. Aufgabe Fourier - Reihen Gegeben sind 3 Funktionen y = f(t) mit der Periodendauer T = 2π durch einen nur im Intervall [-π; π] zutreffenden Ausdruck. Fertigen Sie von allen drei Funktionen eine Skizze für den Bereich t ∈ [-3π ; 3π ] an : 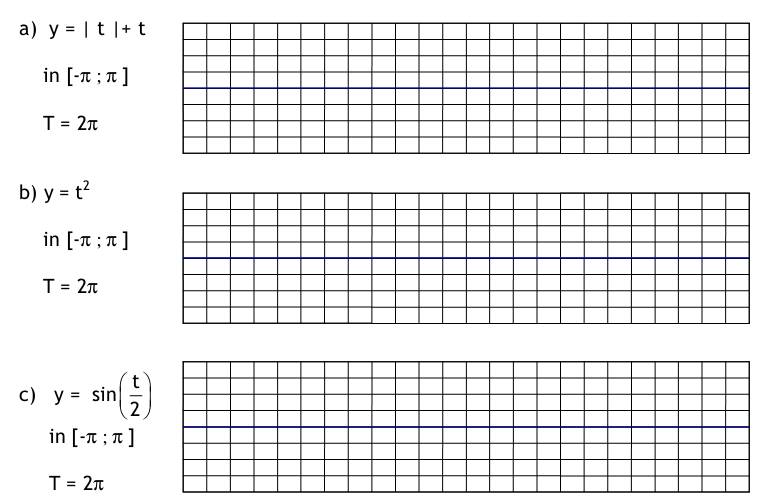 6.2. Bestimmen Sie für alle drei Funktionen den Gleichanteil a0/2 und tragen ihn in die Tabelle ein. Untersuchen Sie, ob die Koeffizienten der reellen Fourierreihe an (cos - Anteile) bzw. bn (sin – Anteile) Null sind, und vermerken das in der nachfolgenden Tabelle durch ja oder nein.  6.3. Berechnen Sie für die unter a) gegebene Funktion die Koeffizienten a2 und b2 der reellen Fourierreihe für die 2. Harmonische (n = 2). Berechnen Sie aus a2 und b2 auch die Koeffizienten A2 und φ2 des Amplituden- und Phasenspektrums. |
| PDF Dokument Aufgaben Beispielklausur |
Diese Seite wurde noch nicht kommentiert.





