Version [58358]
Dies ist eine alte Version von TutoriumMathe3A1 erstellt von Jorina Lossau am 2015-08-27 21:28:39.
Tutorium Mathematik 3
| File | Last modified | Size |
|---|---|---|
| Mathe3.jpg | 2023-10-06 18:37 | 50Kb |
| Mathe3A1.pdf | 2023-10-06 18:37 | 48Kb |
| Mathe3Au1.jpg | 2023-10-06 18:37 | 34Kb |
| Mathe3Aufgaben11.jpg | 2023-10-06 18:37 | 46Kb |
| Mathe3Aufgaben12.jpg | 2023-10-06 18:37 | 49Kb |
| Mathe3Aufgaben13.jpg | 2023-10-06 18:37 | 51Kb |
Anwendungen der Integralrechnung - Aufgaben
| 1) Eine Kette wird zwischen zwei gleich hohen Aufhänge punkten im Abstand l = 5 m befestigt. Gegenüber diesen Punkten hängt sie in der Mitte um d = 3 m durch. Wie lang ist die Kette? 2) Ein Parabolspiegel wird durch die Rotation der Kurve y = k*x² um die y-Achse beschrieben. Wie groß ist seine Oberfläche für k= 1 / m und 0 ≤1 ≤ 1 m (der Parabolspiegel hat also damit einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m). 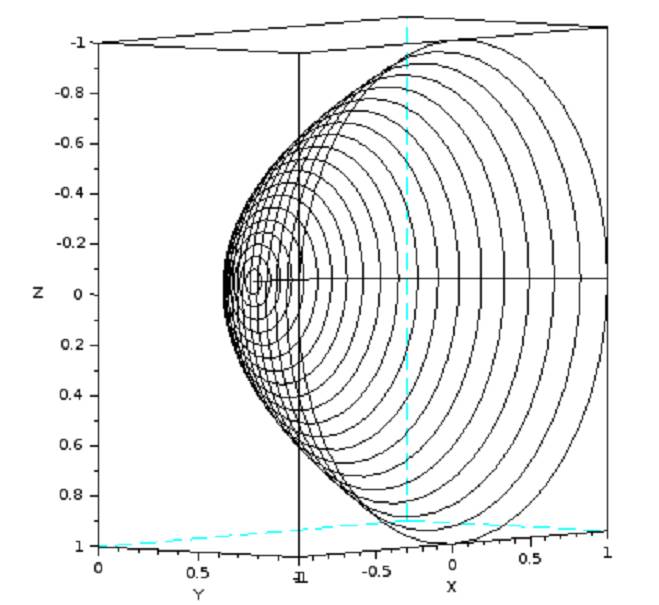 Vergleichen Sie die berechnete Oberfläche mit der einer Halbkugel vom Radius r = 1m (Die Halbkugel hat auch einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m). 3) Während der Zeit T falle ein Strom gemäß einer e-Funktion vom Wert i auf seine Hälfte. Berechnen Sie den integralen Mittelwert und den Effektivwert dieses Stroms in der Zeit T. 4) Ein Körper entsteht durch die Rotation der Kurve sin y = Wurzel von x *sin x um die x-Achse, wobei gilt: 0 ≤ x ≤ π . Berechnen Sie das Volumen des Körpers. Hinweis: Verwenden Sie für das zu lösende Integral die partielle Integration, wobei Sie die Stammfunktion von sin x² aus dem Tabellenbuch entnehmen. |
| PDF Dokument Aufgaben Integralrechnung |
Diese Seite wurde noch nicht kommentiert.





