Version [70418]
Dies ist eine alte Version von Mathe2L5 erstellt von Jorina Lossau am 2016-07-25 13:13:04.
Tutorium Mathematik 2
Extremwerte und Nebenbedingungen, Lagrange Multiplikatoren - Lösungen
| 5.1 Eine zylindrische Blechdose (Radius R, Höhe H) ohne Deckel habe ein Volumen von 1250 ml. Berechnen Sie die Maße der Dose, so dass die not-wendige Lötnaht möglichst kurz ist. (Gelötet wird entlang des kreisförmigen Umfangs der Grundfläche und einmal entlang der Mantellinie der Länge H). - Formulieren Sie Zielfunktion und Nebenbedingung - Berechnung durch Einsetzen der Nebenbedingung in die Zielfunktion - Berechnung durch Lagrange-Multiplikatoren-Methode Lösung: a) Zielfunktion: L(R,H)= 2πR+H Nebenbedingung: g(R,H)=πR^2H-V=0 b) Nebenbedingung nach H umstellen und in Zielfunktion einsetzen: H=V/πR^2 L=2piR+V/πR^2=L(R) Differenzieren der Gleichung: dL/dR=2π-2V/πR^3=0 R^3=V/π^2=1250cm^2/π^2=126,65cm^3 R=3√126,65cm^3 R=5,022cm H=v/πR^2=1250cm^2/π(5,022cm)^2 H=15,777cm d^L/dR^2=6V/πR^4=(6*1250 cm^2)/(π*(5,022cm)^4)=3,75>0-> lokales Minimum c) F(R,H,λ)=2πR+H+λ(πR^2H-V) FR=2π+2λπRH=0 (I) FH=1+λπR^2=0 (II) -> λ = -1/πR^2 in (I) einsetzen Fλ=πR^2H-V=0 (III) -> (2π-2/πR^2)*πRH=0 2π=(2/R)*H H=πR V=πR^2H=πR^2πR=π^2R^3 R=3√(V/π^2)=3√(1250cm^2/π^2)=5,022 cm H=V/πR^2 = 1250 cm^2/π(5,022cm)^2 H= 15,777 cm 5.2 Ein zylinderförmige Dose aus Blech soll ein Volumen von V = 5000cm^3 haben. Zu ihrer Herstellung wird zunächst ein rechteckiges Blech zur Mantelfläche zusammengebogen und entlang der Mantellinie zusammengelötet. Danach werden die kreisrunden Grund- und Deckflächen entlang des jeweiligen Kreisumfangs eingelötet. a) Wie muss die Dose dimensioniert sein (Radius R und Höhe H), damit die Gesamtlänge L der gelöteten Linien minimal ist ? b) Wie muss die Dose dimensioniert sein (Radius R und Höhe H), damit die Oberfläche und damit der Blechverbrauch minimal ist ? Lösung: a) Zielfunktion: L=H+4πR Nebenbedingung: V=πR^2H 1. Weg: Nebenbedingung in Zielfunktion einsetzen L=V/πR^2+4πH=L(R) dL/dR=2V/πR^3+4π=0 4π^2R^3=2V R^3=V/2π^2 R=3√(v/2π^2)=3√(5000 cm^3/2π^2)=6,327 cm H=v/πR^2=39,75 cm Wegen d^2L/dR^2=6V/πR^4>0 ist ein lokales Minimum, d.h. die gelötete Linie ist minimal mit L=39,75 cm+4π*6,327cm=119,26 cm 2. Weg: Lagrange-Multiplikatoren F=L+λ(πR^2H-V) F=H+4πR+λ(πR^2H-V) FH=1+λπR^2=0 (I) FR=4π+2λπRH=0 (II) Fλ=πR^2H-V=0 (III) aus (I) λ=-1/πR^2 in (II) 4π-(2πRH)/(πR^2)=0 4πR^2=2πRH 2πR=H V=πR^2H=πR^2*2πR=2π^2R^3 R^3=V/2π^2 R=6,327cm-> H=2πR=39,75cm Verbale (logische) Begründung für Minimum von L: Lässt man gedanklich die Grundfläche "schrumpfen" (R -> 0), so muss H -> unendlich gehen, damit V=5000cm^3=cost bleiben kann. Lässt man stattdessen H -> 0 gehen, so muss R -> unendlich für V=const. Das bedeutet in beiden Fällen L -> unendlich. Da nur ein Extremwert für L gefunden wird, muss dieser ein Minimum sein. b) Zielfunktion: A = 2πR^2+2πRH Nebenbedingung: V =πR^2H 1. Weg: Nebenbedingung in Zielfunktion einsetzen A= 2πR^2+2πR*V/πR^2=2πR^2+2V/R dA/dR=4πR-2V/R^2=0 4πR^3=2V R^3=V/2π R=3√(V/2π)=3√(5000cm^3/2π)=9,267cm H=V/πR^2 = (5000cm^3)/(π*(9,267cm)^2=18,534cm Es handelt sich tatsächlich um ein Minimum für A, denn: d^2A/dR^2=4π+4V/R^3>0 2. Weg: Lagrange-Multiplikatoren F=2πR^2+2πRH+λ(πR^2H-V) FR=4πR+2πH+λ2πRH=0 (I) FH=2πR+λπR^2=0 (II) Fλ=πR^2H-V=0 (III) aus (II) λ=2πR/πR^2=-2/R in (I) 4πR+2πH-(2/R)2πRH=0 4πR+2πH-4πH=0 2R=H V=πR^2H=πR^2*2R=2πR^3 R^3=V/2π R=3√(V/2π) R=9,267cm -> H=2R=18,534cm 5.3 In eine Kugel mit dem Radius R soll ein Kreiszylinder [ Kreiskegel ] einbeschrieben werden. Bestimmen Sie das Verhältnis von Grundkreisradius und Höhe, wenn das Volumen des Zylinders [ Kegels ] ein Maximum sein soll! Lösung: a) Zylinder ZF: VZylinder = π*r^2*h -> max NB: R^2 = r^2+(h/2)^2 aus NB: r^2=R^2-(h/2)^2 in ZF VZylinder=π(R^2-(h/2)^2)h VZylinder=πR^2h-π/4h^3=f(h) dVZylinder/dh=πR^2-3π/4h^2=0 3π/4h^2=πR^2 h=2/√3*R in NB r^2=R^2-(h/2)^2 r^2=R^2-(3/4R^2)/2^2 r^2=R^2-1/3R^2 r=√(2/3)*R -> r/h=√2/2=0,707 d^2VZylinder/dh^2=0-(3π/2)*h<0 -> max mit Lagrangen Multiplikatoren: F=π*r^2*h+λ(r^2+(h/2)^2-R^2) deltaF/delta r = 2πrh+2λ=0 ->λ=-πh deltaF/delta h = πr^2+1/2λh=0 -> πr^2+1/2(-πh)h=0 -> r^2=h^2/2 in NB: R^2=(h/2)^2+r^2=h^2/4+h^2/2=3h^3/4 -> h=√(4/3)R und r=√(2/3)R 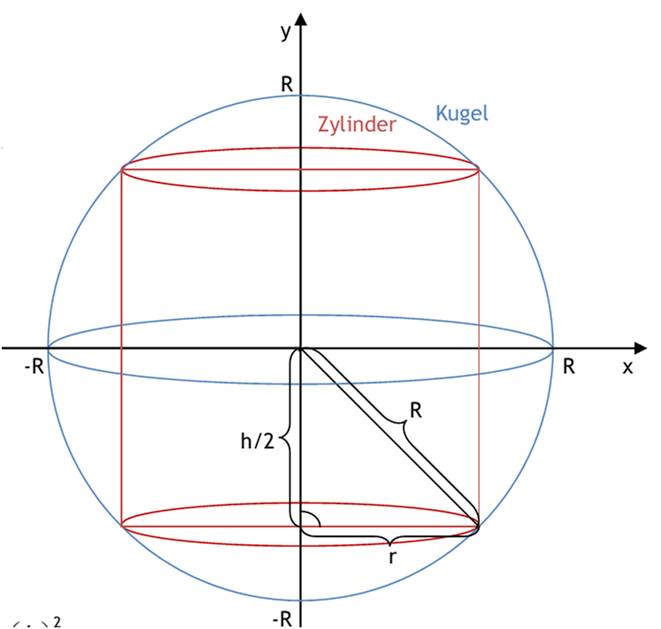 b) Kegel ZF: VKegel = π/3*r^2*h ->max NB: R^2=r^2+(h-R)^2 aus NB: r^2=R^2-(h-R)^2 r^2=R^2-(h^2-2hR+R^2) r^2=2hR-h^2 in ZF VKegel=π/3(2hR-h^2)h VKegel=(2π/3)Rh^2-(π/3)h^3=f(h) dVKegel/dh=(4π/3)RH-ah^2=0 (4π/3)RH=ah^2 I : h (h>0 wegen max.) h=4/3R in NB r^2=R^2-(h-R)^2 r^2=R^2-(4/3R-R)^2 r^2=R^2-1/9R^2 r=√(8/9)R=((√2*2)/3)*R -> r/h=√2/2=rund 0,707 d^2Kegel/dh^2=4π/3R-2πh=4π/3R-2π4/3R<0 -> max mit Lagrangen Multiplikatoren: F=1/3π*r^2*h+λ(r^2+h^2-2hR) deltaF/delta r = 2/3π*r*h+2λr=0 -> λ=-1/3πh deltaF/delta h = 1/3π*r^2+λ(2h-2R)=0 -> 1/3πr^2-1/3πh(2h-2R)=0 I:1/3π -> r^2 = h(2h-2R) mit NB gleichgesetzt: 2hR-h^2=2h^2-2hR I:h -> 4R=3h -> h=4/3R und r=2/3√2R 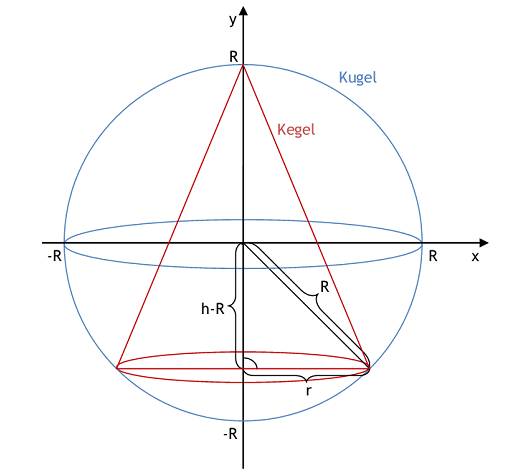 5.4 Ein Körper bestehe aus einem Zylinder mit Grundfläche ( Radius R, Höhe H), auf dem als Deckfläche eine Halbkugel aufgesetzt ist. Man berechne für ein vorgegebenes Volumen V = 1000 cm³ die Werte für R und H so, dass die Oberfläche des Körpers minimal wird! F=3πR^2+2πRH+λ(πR^2H+2/3πR^3-V) deltaF/deltaR=6πR+2πH+λπ(2RH+2RH^2)=0 deltaF/deltaH=2πR+λπR^2=0 ->λ=-2/R in deltaF/deltaR: 6πR+2πH-2/Rπ(2RH+2R^2)=0 I:π 6R+2H-4H-4R=0 H=R ZF: A0 = AHalbkugel+AZyl.Mantel+AZyl.Boden ->min NB: V= VZylinder + VHalbkugel aus ZF: A0=2πR^2+2πRH+πR^2 A0=πR(3R+2H) aus NB: V=πR^2H+1/2(4/3πR^3) V=πR^2H+(2π/3)R^3 H=V-(2π/3R^3)/(πR^2)=v/πR^2-2/3R in ZF A0=πR(3R+2(V/πR^2-2/3R)) A0=3πR^2+2V/R-4π/3R^2=f(R) dA0/dR=6πR-2V/R^2-8π/3R=0 (6π-8π/3)R=2V/R^2 5π/3R^3=V R=3√(3V/5π)=rund5,759cm in NB H=V/πR^2-2/3R=rund 5,759cm d^2A0/dR^2=6π+4V/R^3-8π/3=rund 31,41>0 -> min 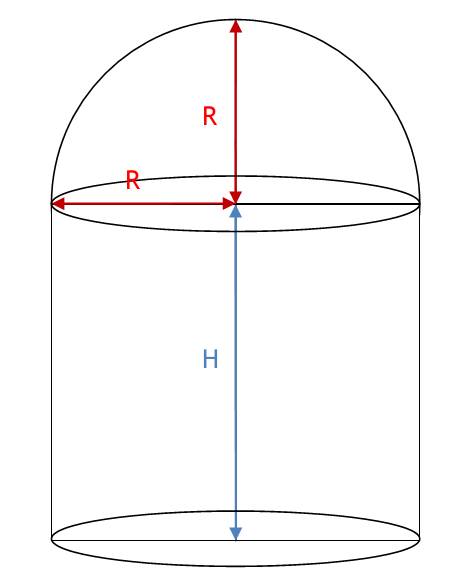 |
| PDF Dokument Lösungen Lagrange |
Diese Seite wurde noch nicht kommentiert.





