Tutorium Statistik/ANOVA

In Bearbeitung

1. Tutor/in:

Johannes Meier
Fakultät Informatik
j.meier@stud.fh-sm.de

2. Ziel des Tutoriums:

- Vorbereitung auf die künftige Statistik-Vorlesung mit Fokus auf einfaktorielle Varianzanalyse (ANOVA - Analysis of Variance)

3. Adressaten des Lehrangebotes:

Studierende der Fakultät Informatik, welche sich vorab einen Einblick in das Thema Varianzanalyse verschaffen möchten.

4. Veranstaltungsdatum/-zeit/-ort:

Termine finden nach Absprache statt


5. Literaturhinweise:



6. Aufgaben:

in Bearbeitung

7. Historischer Einblick:

„Sir Ronald Aylmer Fisher (1890-1962) veröffentlichte erstmals 1935 in „The Design of Experiments“ eine umfassende Darstellung der Versuchsplanung mit den Grundlagen der Varianzanalyse. Er war am Rothamstead Agriculture Insititute beschäftigt und sollte sich als einer der fruchtbarsten praktischen Statistiker dieses Jahrhunderts erweisen. Als dann George W. Snedecor (1881-1974) die später Fisher zu Ehren benannte F-Verteilung veröffentlichte, konnte eine umfassende Theorie der ein- und mehrfachen, hierarchischen und faktoriellen, Varianzanalyse entstehen.
Die statistische Testtheorie nahm mit Jerzy Neyman (1894-1981), Egon Sharpe Pearson (1895-1980), Sohn von Karl Pearson, und Abraham Wald (1902-1950) einen bedeutenden Aufschwung und entwickelte sich zu dem, was wir heute benutzen.“ [0]
Varianzanalyse (ANOVA) ist ein Verfahren, das die Wirkung einer (oder mehrerer) unabhängiger Variablen auf eine (oder mehrere) abhängige Variablen untersucht.
Bei unabhängigen Variablen wird dabei lediglich Nominalskalierung verlangt, sodass sie keine natürliche Reihenfolge aufweisen müssen. Abhängige Variablen hingegen besitzen metrisches Skalenniveau, Gruppen sind so klar erkennbar. Die Varianzanalyse ist das wichtigste Analyseverfahren bei der Auswertung von Experimenten. [1]
Im Folgenden wird sich (derzeit noch) auf die einfaktorielle ANOVA beschränkt.

8. Einfaktorielle ANOVA

Von einer einfaktoriellen ANOVA spricht man, wenn lediglich eine einzige abhängige und metrisch skalierte Variable sowie eine unabhängige nominal skalierte Variable gegeben ist.
Der Einfluss von einer unabhängigen auf eine abhängige Variable kann so untersucht werden. [2]

Jede ANOVA beginnt zunächst mit einer Problemstellung, welche zuletzt beantwortet wird.
Diese Interpretation wird später genauer beschrieben.

9. Problemstellung

Die Problemstellung beschreibt alle relevanten Einflussgrößen, die es gilt mit der ANOVA zu interpretieren. Einflussgrößen werden mit allen Messwerten tabellarisch aufgezeigt. Ein Beispiel wäre hier die Verträglichkeit eines Medikaments, welches mehreren Probandengruppen verabreicht wird. Die Gruppen hingegen unterscheiden sich nochmals in den Lebensjahren (Heranwachsender, Erwachsener, Senior). Über die ANOVA ist zu klären, ob das Lebensalter der Probandengruppen einen Einfluss darauf hat, wie das Medikament vertragen wird.
Als abhängige Variable ist im Beispiel die „Verträglichkeit des Medikaments“ (metrisch skaliert) gemeint, welche auf die unabhängige Variable „Lebensalter“ (nominal skaliert) mit den drei Ausprägungsstufen (Heranwachsender, Erwachsener, Senior) durch die ANOVA analysiert werden soll.


10. Streuungsbereich

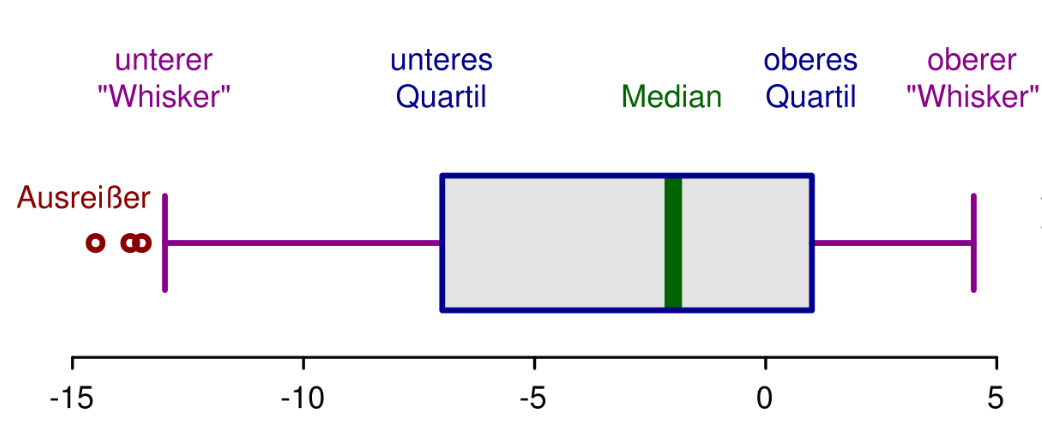
Bei Messungen kann es vorkommen, dass sich ein Messfehler einschleicht oder eine Zahl falsch notiert wurde. Dies fällt dann besonders auf, wenn ein einzelner Wert der Zufallsstichprobe weit außerhalb des normalen Streubereichs liegt. [3]
Den Streubereich kann man leicht mithilfe des Werteintervalls (range) und des Interquartilsabstands (IQR, inter-quartile range) definieren. Der Messwerteintervall ist die Länge des kleinsten Intervalls, das alle Beobachtungswerte enthält. Der IQR ist die Länge des Intervalls, das die mittlere Hälfte der Daten enthält. [7]
Für die Bildung der Percentile werden die Daten der Größe nach geordnet.
Der minimale Wert ist das nullte Percentil und das Maximum das 100. Percentil.
Das erste Percentil ist der Wert des Stichprobenelementes, welches bei einem Prozent des Stichprobenumfanges liegt.
Das erste Quartil teilt den Wertebereich in das erste Viertel ein und ist gleich dem 25. Percentil.
Der Werteberiech entspricht somit der Differenz von Maximum und Minimum, das heißt des 100. und des nullten Percentils.



Das Intervall

formel

[Q_1;Q_3]

formel

wird auch als „mittlerer 50%-Bereich“ bezeichnet. Liegt ein Wert nun außerhalb des Intervalls der Antennen, spricht man von sogenannten Ausreißern.

Bei milden Ausreißer gilt:




Bei extremen Ausreißer gilt:




Diese Art von Festlegung der Antennen hat den Nachteil, dass es sich auf die Annahme auf eine Normalverteilung bezieht.
Trotzdem kann ein vom Mittelwert weit entfernt liegender Wert in Wirklichkeit zum Kollektiv gehören, deshalb sollten Ausreißer zunächst behalten werden.
Alle Werte innerhalb des Intervalls sind somit innerhalb des Streubereichs.




Zur Bestimmung des Streuungsbereichs ist es notwendig quadratische Abweichungen (sum of squares - SS) zu berechnen, auf die im nächsten Abschnitt näher eingegangen wird.

Als Beobachtungswert wird im Folgenden anstelle von x, y verwendet.

11. Quadratische Abweichungen




Mittelwerte

Zur Bestimmung der quadratischen Abweichungen müssen diverse Mittelwerte bestimmt werden.
Beginnend mit dem Gesamtmittelwert, welcher Quotient aus der Summe aller Messwerte und der Anzahl der Beobachtungen ist [1], müssen zusätzlich die Mittelwerte der einzelnen Gruppen bestimmt werden. [2].




Mit den oben aufgeführten Mittelwerten lassen sich die zugehörigen Daten zentrieren und ihre quadratische Abweichung vom Wert 0 (Zentrum) berechnen.

Quadratsummen

Die Quadratsumme der Abweichungen als Maß für die Streuung wird umso größer, je größer die Zahl der Einzelwerte ist.
Varianz ist das zentrale Moment zweiter Ordnung einer Zufallsvariablen.
Sie ist im Allgemeinen unbekannt, weil der Typ und die Ausprägung der Wahrscheinlichkeitsdichtefunktion nicht bekannt sind. Sie kann durch die empirische Varianz geschätzt werden, bei der unter der Annahme einer repräsentativen Stichprobe und einer Normalverteilung die Abweichungsquadrate summiert werden (sum of squares) und durch die Anzahl der Freiheitsgrade n-1, wobei n die Anzahl der Beobachtungen ist, dividiert wird.
Um eine aussagekräftige Schätzgröße für die Streuung zu erhalten, berechnen wir die Varianz. Die Varianz ist unabhängig von der Zahl der Beobachtungswerte und wird auch als empirische Varianz bezeichnet.




Eine Varianz, in die alle Elemente der Grundgesamtheit einfließen, sei als empirische Varianz bezeichnet. Beschränkt sich die statistische Erhebung dagegen nur auf einen Teil der Grundgesamtheit, ist die Varianz eine Stichprobenvarianz.

In einer empirischen Varianz wird die durchschnittliche Merkmalsausprägung aus allen Merkmalsausprägungen der Grundgesamtheit ermittelt. Eben deswegen ist dieser Wert der richtig ermittelte Durchschnitt, die wahre durchschnittliche Merkmalsausprägung. [4]
Das zuletzt zu bestimmende Konfidenzintervall setzt die folgenden Quadratsummen voraus.
Allgemein ist die empirische Varianz definiert als mittlere quadratische Abweichung vom empirischen Erwartungswert (mean sum of squares). [5]

Gesamtquadratsumme (sum of squares total – SST) ist wie folgt definiert:




Quadratsumme innerhalb der Gruppen (sum of squares within – SSW) ist wie folgt definiert:




Quadratsumme zwischen den Gruppen (sum of squares between – SSB) ist wie folgt definiert:




Die Mittlere quadratische Gesamtabweichung (MST – mean square of treatments) ist wie folgt definiert:




Die Mittlere quadratische Abweichung zwischen den Faktorstufen (MSB - mean square between) ist wie folgt definiert:




Die Mittlere quadratische Abweichung innerhalb der Faktorstufen (MSW – mean square within) ist wie folgt definiert:




12. Freiheitsgrade:

Die Freiheitsgrade setzen sich jeweils aus den Nennern von MST, MSW und MSB zusammen, während MST die Summe aus MSW und MSB ist.

13. Statistische Unabhängigkeit:

Zur Prüfung der statistischen Unabhängigkeit ist es notwendig MSB und MSW in Beziehung zu setzen, um den empirischen F-Wert zu erhalten.
Dieser soll Aufschluss darüber geben, ob die vorab beschriebene Problemstellung (Hypothese) angenommen oder verworfen werden soll.




14. Hypothesen:

„Den Maßstab zur Beurteilung des empirischen F-Wertes bildet die theoretische F-Verteilung. Ausgangspunkt der Prüfung ist die Nullhypothese〖 H〗_0.“[6]
Die Nullhypothese sagt aus, dass es keine Unterschiede zwischen den Gruppen gibt.
Die Alternativhypothese H_1 hingegen, beschreibt Unterschiede.

Formal lautet die Fragestellung des F-Tests:




14. Konfidenzintervall:

Es ist relativ unwahrscheinlich, dass die Ergebnisse von Stichproben genau mit der Grundgesamtheit übereinstimmen.
Gewiss wird mal die eine oder andere Stichprobe ein mit der Grundgesamtheit übereinstimmendes Ergebnis liefern – aber es ist genauso gut möglich, dass es gewisse Abweichungen gibt. Da wir normalerweise nur eine Stichprobe vorliegen haben, wissen wir nicht, ob sie mit der Grundgesamtheit gut übereinstimmt oder nicht.
Sicheres Wissen über die Grundgesamtheit kann man also anhand von Stichprobendaten grundsätzlich nicht erhalten. Jedoch kann man mit Hilfe statistischer Überlegungen einen Bereich angeben, der den Wert der Grundgesamtheit wahrscheinlich enthält.
Diese Wertebereich nennt man Konfidenzintervall. [7]
In der Regel wird ein Konfidenzintervall von 99% oder 95% und somit ein Signifikanzniveau von 1% bzw. 5% gewählt.
Die zu prüfende Stichprobe wird auch als empirischer F-Wert F_emp bezeichnet.

15. Interpretation:

Anhand einer entsprechenden Tabelle der theoretischen F-Werte lässt sich nun ein Wert ablesen, welchen es gilt zu interpretieren.
Der vorab berechnete F-Wert F_emp soll anhand einer Grafik veranschaulicht werden, um die Annahme einer der beiden Hypothesen beantworten zu können.




Liegt F_emp nun innerhalb des Annahmebereichs, wird die Nullhypothese angenommen und alle Faktoren als statistisch unabhängig angesehen.

---

CategoryTutorienFKITWS1819