Tutorium Mathematischer Grundkurs
Gleichungen und Ungleichungen für eine Variable
| Äquivalenzumformungenlassen die Lösungsmenge unverändert. Dazu gehört: 1. Es wird auf beiden Seiten dasselbe addiert oder subtrahiert. „Dasselbe“ kann eine beliebige Zahl sein (z.B. 13) oder eine Variable (z.B. x) oder auch ein komplizierterer Ausdruck (z. B. (2x – 4)). 2. Beide Seiten der Gleichung werden mit demselben multipliziert. Hier muss man aufpassen, dass man nicht mit Null multipliziert. Dabei wird nämlich sogar eine falsche Gleichung richtig, nämlich zu 0 = 0, und das darf nicht passieren. (auch nicht aus Versehen: bei Multiplikation mit (2x – 4) würde man nämlich dann mit Null multiplizieren haben, wenn x gerade 2 wäre) 3. Beide Seiten der Gleichung werden durch dasselbedividiert, wobei man auch nicht durch Null dividieren darf! Quadratische Gleichungenbringt man in die Normalform: x²+px+q = 0 und löst sie mit der auswendig gelernten Formel 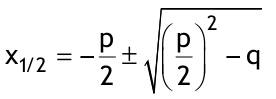 Bei Wurzelgleichungenwerden die Wurzeln i.a. durch Quadrieren beseitigt. (Weil Quadrieren keine Äquivalenzoperation ist, muss man am Ende stets eine Probe machen.) √(x+2)+√(x-3) = 5 Vor dem Quadrieren die Wurzeln „gleichmäßig“ verteilen verringert oft den Aufwand √(x+2) = 5-√(x-3) I (...)² x+2 = 25-10√(x-3)+x-3 10√(x-3) = 20 √(x-3) = 2 I (...)² x-3 = 4 x= 7 Die Probe zeigt, dass diese Lösung stimmt. |
| PDF Dokument Gleichungen und Ungleichungen für eine Variable |
Diese Seite wurde noch nicht kommentiert.





