Version [60358]
Dies ist eine alte Version von TutoriumMathe3L7 erstellt von Jorina Lossau am 2015-10-16 21:18:11.
Tutorium Mathematik 3
Lineare Inhomogene Differentialgleichungen mit konstanten Koeffizienten - Lösungen
| File | Last modified | Size |
|---|---|---|
| KonstanteL1.jpg | 2023-10-06 18:37 | 9Kb |
| KonstanteL10.jpg | 2023-10-06 18:37 | 6Kb |
| KonstanteL11.jpg | 2023-10-06 18:37 | 7Kb |
| KonstanteL12.jpg | 2023-10-06 18:37 | 2Kb |
| KonstanteL13.jpg | 2023-10-06 18:37 | 7Kb |
| KonstanteL14.jpg | 2023-10-06 18:37 | 9Kb |
| KonstanteL15.jpg | 2023-10-06 18:37 | 13Kb |
| KonstanteL16.jpg | 2023-10-06 18:37 | 3Kb |
| KonstanteL17.jpg | 2023-10-06 18:37 | 6Kb |
| KonstanteL18.jpg | 2023-10-06 18:37 | 12Kb |
| KonstanteL19.jpg | 2023-10-06 18:37 | 16Kb |
| KonstanteL2.jpg | 2023-10-06 18:37 | 3Kb |
| KonstanteL20.jpg | 2023-10-06 18:37 | 3Kb |
| KonstanteL21.jpg | 2023-10-06 18:37 | 10Kb |
| KonstanteL22.jpg | 2023-10-06 18:37 | 3Kb |
| KonstanteL23.jpg | 2023-10-06 18:37 | 2Kb |
| KonstanteL24.jpg | 2023-10-06 18:37 | 11Kb |
| KonstanteL25.jpg | 2023-10-06 18:37 | 12Kb |
| KonstanteL26.jpg | 2023-10-06 18:37 | 19Kb |
| KonstanteL27.jpg | 2023-10-06 18:37 | 10Kb |
| KonstanteL28.jpg | 2023-10-06 18:37 | 7Kb |
| KonstanteL29.jpg | 2023-10-06 18:37 | 8Kb |
| KonstanteL3.jpg | 2023-10-06 18:37 | 4Kb |
| KonstanteL30.jpg | 2023-10-06 18:37 | 7Kb |
| KonstanteL31.jpg | 2023-10-06 18:37 | 6Kb |
| KonstanteL4.jpg | 2023-10-06 18:37 | 5Kb |
| KonstanteL40.jpg | 2023-10-06 18:37 | 5Kb |
| KonstanteL41.jpg | 2023-10-06 18:37 | 7Kb |
| KonstanteL42.jpg | 2023-10-06 18:37 | 8Kb |
| KonstanteL43.jpg | 2023-10-06 18:37 | 11Kb |
| KonstanteL44.jpg | 2023-10-06 18:37 | 5Kb |
| KonstanteL45.jpg | 2023-10-06 18:37 | 12Kb |
| KonstanteL46.jpg | 2023-10-06 18:37 | 10Kb |
| KonstanteL47.jpg | 2023-10-06 18:37 | 8Kb |
| KonstanteL5.jpg | 2023-10-06 18:37 | 9Kb |
| KonstanteL6.jpg | 2023-10-06 18:37 | 4Kb |
| KonstanteL7.jpg | 2023-10-06 18:37 | 16Kb |
| KonstanteL8.jpg | 2023-10-06 18:37 | 6Kb |
| KonstanteL9.jpg | 2023-10-06 18:37 | 10Kb |
| Mathe3L7.pdf | 2023-10-06 18:37 | 79Kb |
| Mathe3L71.jpg | 2023-10-06 18:37 | 114Kb |
| Mathe3L72.jpg | 2023-10-06 18:37 | 73Kb |
| Mathe3L73.jpg | 2023-10-06 18:37 | 109Kb |
| Mathe3L74.jpg | 2023-10-06 18:37 | 52Kb |
| Mathe3L75.jpg | 2023-10-06 18:37 | 75Kb |
| Mathe3L76.jpg | 2023-10-06 18:37 | 97Kb |
| Mathe3L77.jpg | 2023-10-06 18:37 | 89Kb |
| Mathe3L78.jpg | 2023-10-06 18:37 | 59Kb |
| Mathe3L79.jpg | 2023-10-06 18:37 | 64Kb |
| 1.4 Lineare inhomogene Differentialgleichungen mit konstanten Koeffizienten Aufgabe 1.4.1  a) Unter welcher Bedingung beschreibt die zugehörige homogene DGL eine ungedämpfte Schwingung wenn a > 0 bekannt ist ? Die charakteristische Gleichung mit ihren Lösungen lautet: 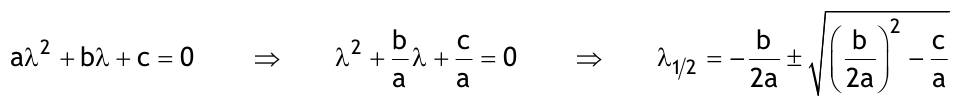 Die zugehörige homogene DGL beschreibt eine ungedämpfte Schwingung für den Fall, dass die Lösung ihrer charakteristischen Gleichung rein imaginäre konjugiert komplexe λ enthält. Dies ist der Fall wenn sowohl b = 0 ist (es liegt dann keine 1. Ableitung von y vor) als auch c dasselbe Vorzeichen wie a hat, also c > 0 ist b = 0 und c > 0 b) Unter welcher Bedingung beschreibt die zugehörige homogene DGL eine gedämpfte Schwingung wenn a > 0 bekannt ist? Auch hier müssen die Lösungen der charakteristischen Gleichung konjugiert komplexe λ – Werte sein, was unter der Wurzel einen negativen Ausdruck erfordert. Außerdem muss der Realteil negativ sein, was wegen a > 0 auch b > 0 erfordert.  c) Lösen Sie die DGL für den Fall a = 2, b = 16, c = 30 und y(0) = 2, y°(0) = 5 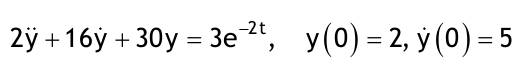 homogene Lösung: 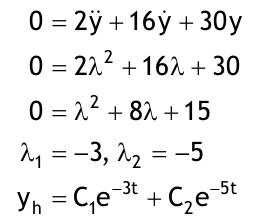 partikuläre Lösung: 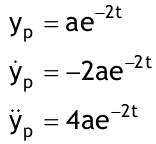 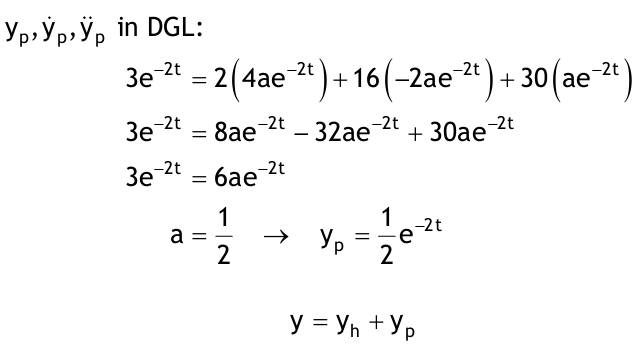 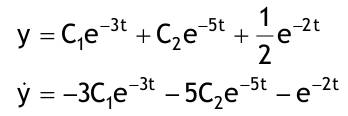 = allgemeine Lösung 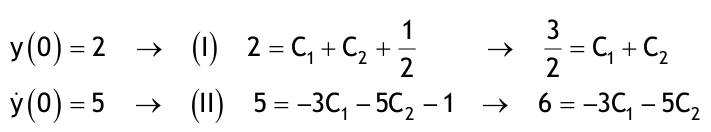 nach Lösung des LGS: 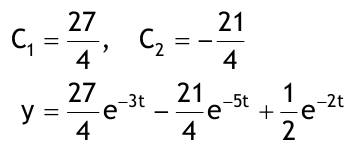 = spezielle Lösung d) Unter welchen Bedingungen würde man bei der inhomogenen DGL ay°° + by° + cy = 3e^(-2t) von „mathematischer Resonanz“ sprechen? Man spricht von „mathematischer Resonanz“, wenn dieStörfunktion S (x) selbst eine Lösung der zugehörigen homogenen DGL ist. Eine Teillösung der zugehörigen homogenen DGL muss also eine ebensolche Exponentialfunktion mit dem Koeffizienten α = − 2 im Exponent sein. Das ist der Fall, wenn die charakteristische Gleichung mindestens eine reelle Lösung λ1 = −2 aufweist. Damit lässt sich die charakteristische Gleichung inder Produktform aufschreiben nd in die Summenform bringen und dann mit der zug.hom. DGL vergleichen: 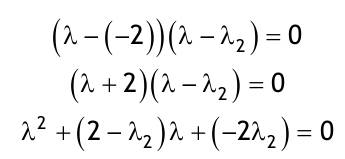 Vergleich mit charakteristischer Gleichung liefert: 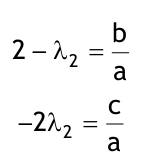 Auflösen nach und Gleichsetzen liefert schließlich: 4a + c = 2b Unter der Bedingung 4a + c = 2b wird sich also stets (mindestens) ein λ = −2 ergeben, so dass die Störfunktion S (x) = 3e^(-2t) zu mathematischer Resonanz führt. e) Finden Sie eine allgemeine Lösung für den Fall a = 1, b = 5 und c = 6 homogene Lösung: 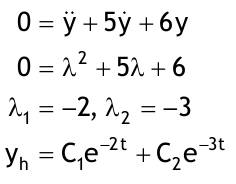 partikuläre Lösung: Es tritt Resonanz auf; 2 ist eine einfache Nullstelle im Lambda - Ansatz! 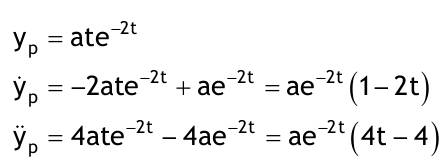 yp, y°p, y°°p in DGL: 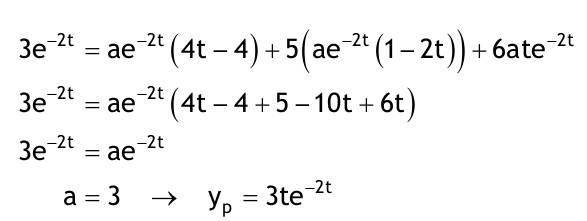 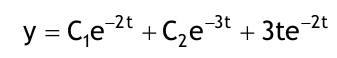 = allgemeine Lösung f) Finden Sie die spezielle Lösung für den Fall a = 1, b = 4, c = 4 und y(0) = 2, y°(0) = 5 homogene Lösung: 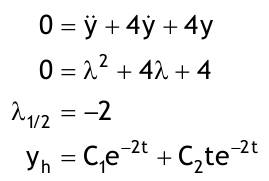 partikuläre Lösung: Es tritt Resonanz auf; -2 ist eine doppelte Nullstelle im Lambda - Ansatz! 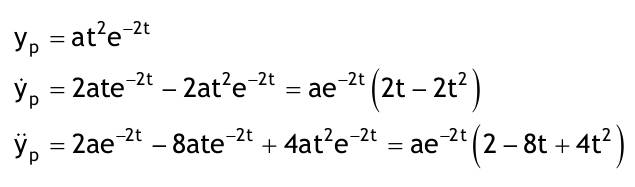 yp, y°p, y°°p in DGL: 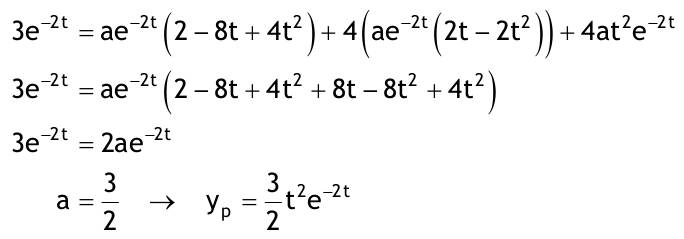 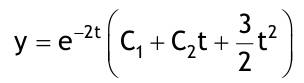 = allgemeine Lösung 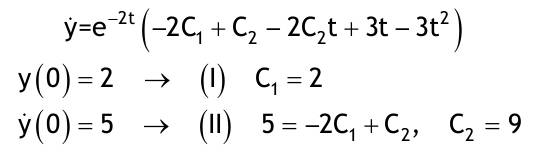 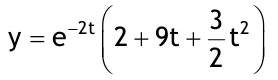 = spezielle Lösung Aufgabe 1.4.2 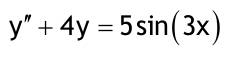 homogene Lösung: 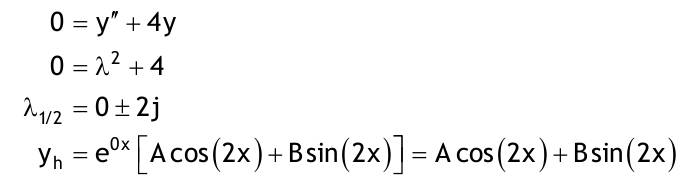 partikuläre Lösung: 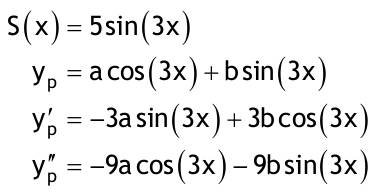 yp, y°°p in DGL: 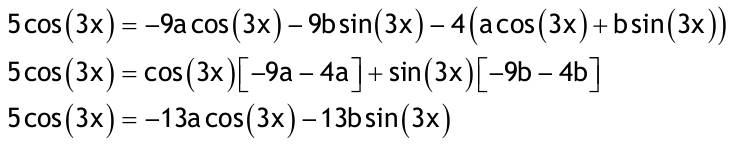 Koeffizientenvergleich: sin(3x) = 0 = -13b --> b = 0 cos(3x) = 5 = -13a --> a = -5/13 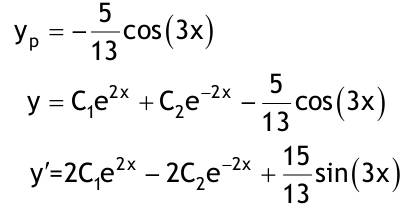 = allgemeine Lösung a) Anfangswerte:y(0) = 2, y'(0) = -3 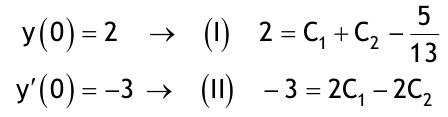 Lösung des LGS: 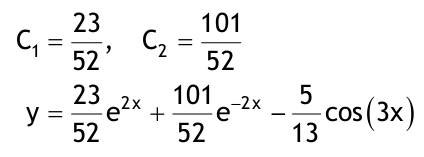 = spezielle Lösung b) Anfangswerte:y(0) = y'(0) = 0 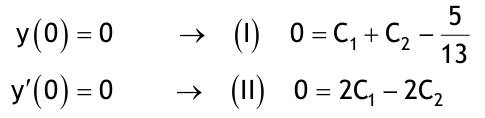 Lösung des LGS: 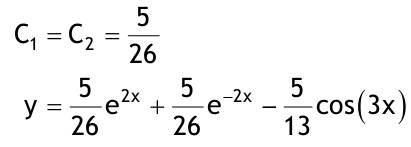 Aufgabe 1.4.3 b) Anfangswerte: y(0) = y'(0) = 0 Aufgabe 1.4.4  |
| PDF Dokument Inhomogene Differentialgleichungen |
Diese Seite wurde noch nicht kommentiert.





