Tutorium Mathematik 3
Differentialgleichungen - Lösungen
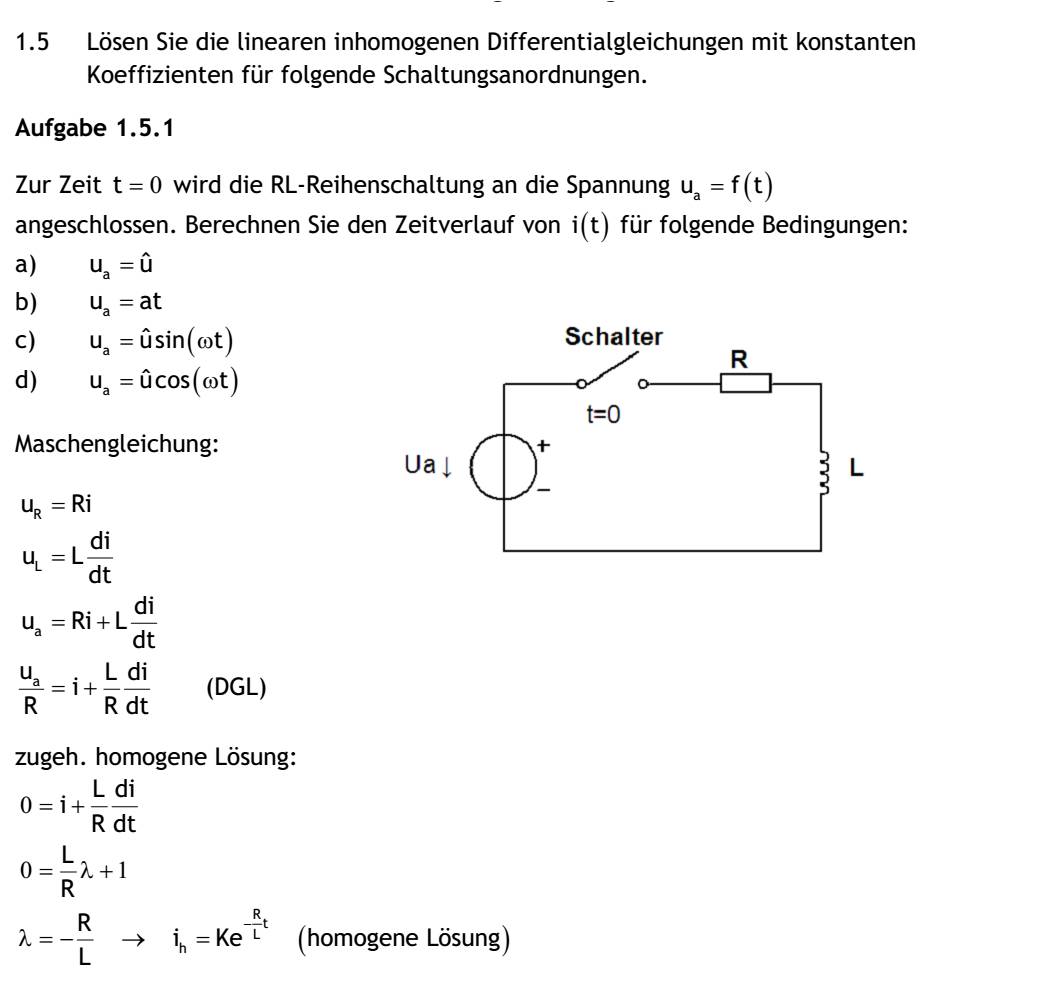




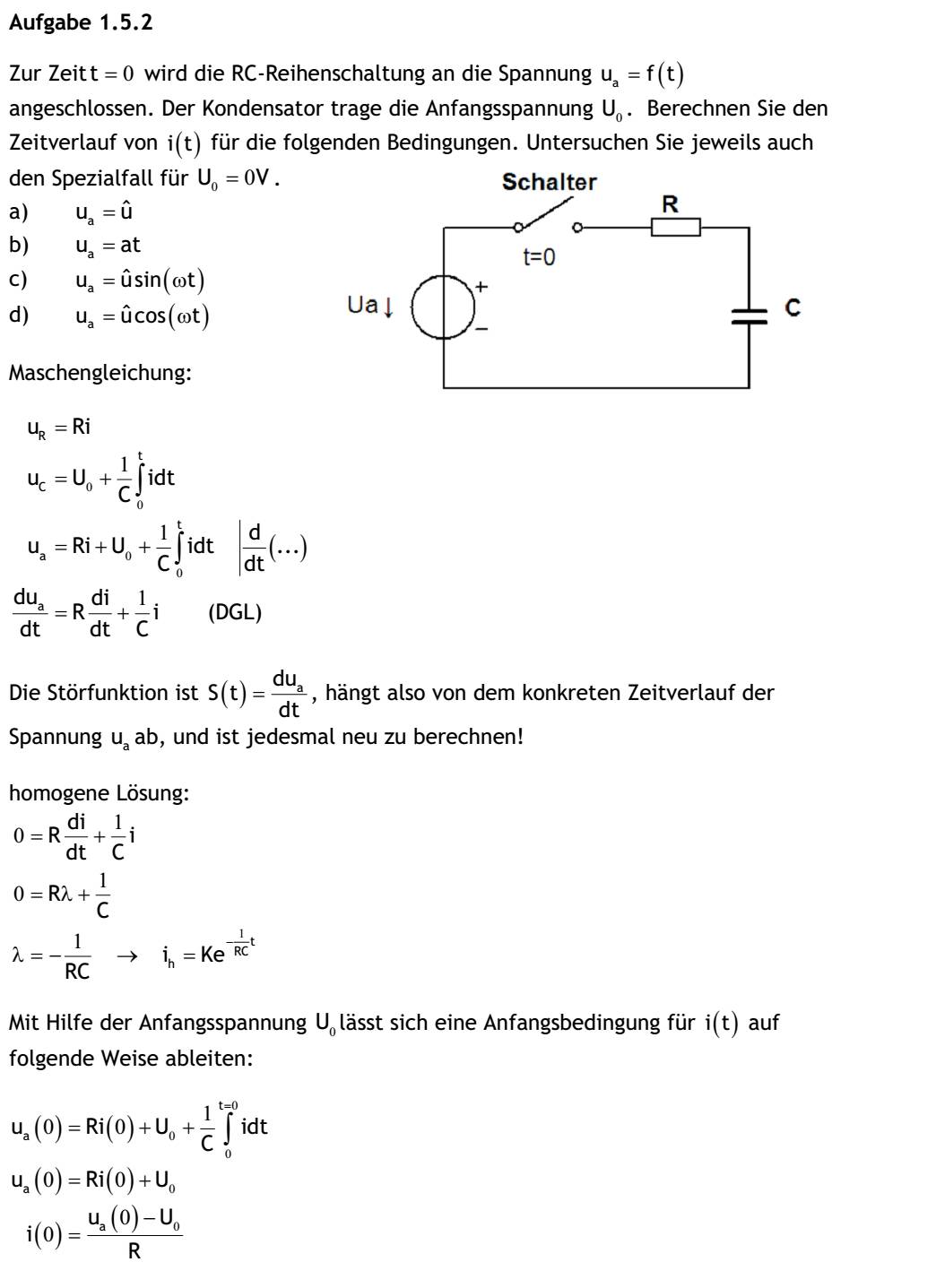
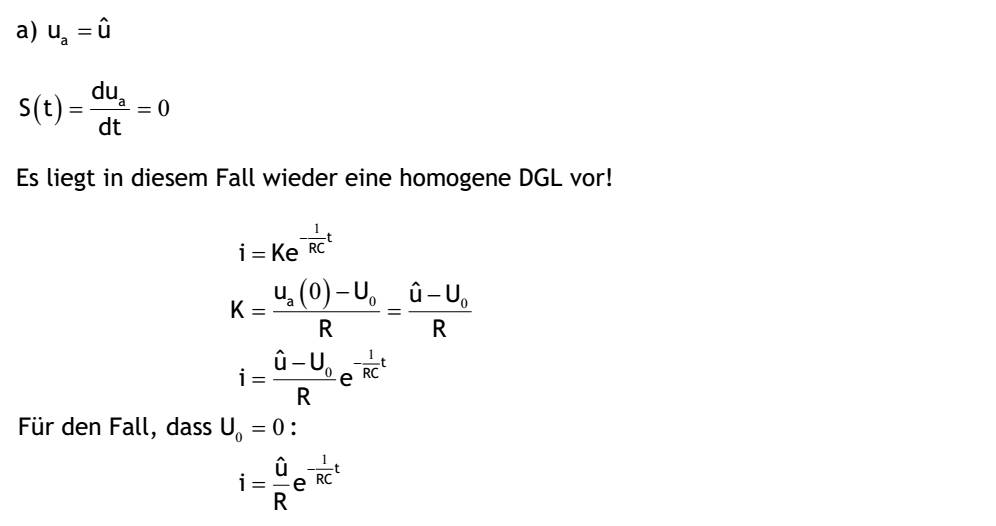


| 1.5 Lösen Sie die linearen inhomogenen Differentialgleichungen mit konstanten Koeffizienten für folgende Schaltungsanordnungen. Aufgabe 1.5.1 Zur Zeit t=0 wird die RL-Reihenschaltung an die Spannung Ua=f(t) angeschlossen. Berechnen Sie den Zeitverlauf von i(t) für folgende Bedingungen: a) ua=u^ b) ua=at c) ua=u^sin(wt) d) ua=u^cos(wt) Maschengleichung: uR=Ri uL=L(di/dt) ua=Ri+L(di/dt) ua/R=i+(L/R)*(di/dt) zugeh. homogene Lösung: 0=i+(L/R)*(di/dt) U=(L/R)λ+1 λ=-R/L->ih=ke^((-R/L)t) (hom. Lösung) a) Ua=u^ partikuläre Lösung: u^/R=i+(L/R)*(di/dt) ip=A dip/dt=0 ip, dip/dt in DGL: u^/R=A+(L/R)*0 A=u^/R ip=u^/R i=ih+ip i=ke^((R/L)*t)+u^/R mit Anfangsbed. i(0)=0 0=K+u^/R K=-u^/R i(t)=-(u^/R)e^((R/L)t)+u^/R b) ua=at partikuläre Lösung: at/R=i+(L/R)*(di/dt) ip=At+B dip/dt=A ip,dip/dt in DGL: at/R=At+B+(L/R)*A t:A=a/R t0:0=B+(L/R)*A -> 0=B+(L/R)*(a/R)-> B=-La/R^2 ip=(a/R)*t-La/R^2 i=ih+ip i=ke^((R/L)*t)+(a/R)*t-(La)/(R^2) mit Anfangsbedingung i(0)=0 0=K-La/R^2 K=La/R^2 i(t)=(a/R)t-La/R^2(1-e^((-R/L)t) c) ua=u^sin(ωt) partikuläre Lösung: (u^sin(ωt))/R=i+(L/R)*(di/dt) ip=Acos(ωt)+Bsin(ωt) dip/dt=-Aωsin(wt)+Bωcos(ωt) ip, dip/dt in DGL: (u^sin(ωt))/R=Acos(ωt)+Bsin(ωt)+L/R(-Aωsin(ωt)+Bωcos(ωt)) sin(ωt): 1: u^/R=B-(LAω)/R cos(ωt): 2: 0=A+(LBω)/R nach Lösung des GLS: A=(-Lωu^)/((Lω)^2+R^2), B=Ru^/((Lω)^2+R^2) ip=(-Lωu^)/((Lw)^2+R^2)cos(ωt)+Ru^/((lω)^2+R^2)sin(ωt) i=ih+ip i=ke^(-R/L)*t)-Lωu^/((Lω)^2+R^2)cos(ωt)+Ru^/((Lω)^2+R^2)sin(ωt) mit Anfangsbedingung i(0)=0 u=K- (Lωu^)/((Lω)^2+R^2) K=Lωu^/((Lω)^2+R^2) i(t)=Lωu^/((Lω)^2+R^2)e^((-R/L))t-Lωu^/((Lω)^2+R^2)cos(ωt)+Ru^/((Lω)^2+R^2)sin(ωt) i(t)=u^/(√(R^2-(Lω)^2)(Lω/(√(R^2+(Lω)^2)sin(ωt)) d) ua=u^cos(ωt) partikuläre Lösung: u^cos(ωt)/R=i+(L/R)*(di/dt) ip=Acos(ωt)+Bsin(ωt) dip/dt=-Aωsin(ωt)+Bωcos(ωt) ip,dip/dt in DGL: u^cos(ωt)/R=Acos(ωt)+Bsin(ωt)+L/R(-Aωscosin(ωt)+Bωcos(ωt)) sin(ωt): 1: 0=B-LAω/R nach Lösung des LGS: A=Ru^/((Lω)^2+R^2), B=Lωu^/((Lω)^2+R^2 ip=Ru^/((Lω)^2+R^2)cos(ωt)+((Lωu^)/((Lω)^2+R^2))sin(ωt) i=ih+ip i=Ke^(-R/L)t+Ru^/((Lω)^2+R^2)cos(ωt)+(Lωu^/((Lω)^2+R^2))sin(ωt) mit Anfangsbedingung i(0)=0 0=K+ K=-(Ru^/(Lω)^2+R^2) i(t)=-(Ru^/(Lω)^2+R^2)e^((-R/L)t)+Ru^/(Lω)^2+R^2)cos(ωt)+Lωu^/((Lω)^2+R^2)sin(ωt) i(t)=u^/(√(R^2+(Lω)^2)(-R/(√(R^2+(Lω)^2)e^((-R/L)t)+R/(√(R^2+(Lω)^2)cos(ωt)+Lω/(√(R^2+(Lω)^2)sin(ωt)) Aufgabe 1.5.2 Zur Zeit t=0 wird die RC-Reihenschaltung an die Spannung ua=f(t) angeschlossen. Der Kondensator trage die Anfangsspannung U0. Berechnen Sie den Zeitverlauf von i(t) für die folgenden Bedingungen. Untersuchen Sie jeweils auch den Spezialfall für U0=0V. a) ua=u^ b) ua=at c) ua=u^sin(ωt) d) ua=u^cos(ωt) Maschengleichung: uR=Ri uC=Uu+1/C∫idt wobei ∫ von 0 bis t ua=Ri+U0+1/C∫idt wobei ∫ von 0 bis t Id/dt (...) dua/dt=R(di/dt)+1/Ci(DGL) Die Störfunktion ist s(t)=dua/dt, hängt also von dem konkreten Zeitverlauf der Spannung ua ab, und ist jedesmal neu zu berechnen! homogene Lösung: 0=R(di/dt)+1/Ci 0=Rλ+1/C λ=-1/(RC) -> ih=Ke^(-1/(RC)t) Mit Hilfe der Anfangsspannung U0 lässt sich eine Anfangsbedingung für i(t) auf folgende Weise ableiten: ua(0)=Ri(0)+U0+1/C∫idt wobei ∫ von 0 bis t=0 ua(0)=Ri(0)+U0 i(0)=(ua(0)-U0)/R) a) ua=u^ S(t)=dua/dt=0 -> homogene DGL i=Ke^((-1/RC)t) K=(ua(0)=U0/R=((u^-U0)/R) i=((u^-U0)/R)e^((-1/RC)t) für den Fall, dass U0=0: i=(u^/R)e^((-1/RC)t b)ua=at, partikuläre Lösung S(t)=dua/dt=a a=R(di/dt)+(1/C)i ip=A dip/dt=0 ip,dip/dt in DGL: a=R*U+(1/C)A A=Ca ip=Ca i=ih+ip i=Ke^(-1/RC)tCa mit i(0)=(ua(0)-U0)/R, i(0)=K+Ca K+Ca=(0-U0)/R wegen ua(0)=0 K=-(U0/R+Ca) i=-e^((-1/RC)t)(U0/R+Ca)+Ca i=Ca(1-e^((-1/RC)t))-(U0/R)e^((-1/RC)t) für den Fall, dass U0=0: i=Ca(1-e^((-1/RC)t) Nach genügend langer Zeit würde ein konstanter Strom i=Ca=const. fließen. Praktisch steigt die Spannung am Kondensator dann auch etwa linear mit der Zeit (bis seine Spannungsfestigkeit überschritten ist). c) ua=u^sin(wt) d(û^sin(wt))/dt=R(di/dt)+(1/C)i u^ωcos(ωt)=R(di/dt)+(1/C)i partikuläre Lösung: ip=Acos(ωt)+Bsin(ωt) (dip)/dt=-Aωsin(ωt)+Bωcos(ωt) ip,(dip)/dt in DGL: u^ωcos(ωt)=R(-Aωsin(ωt)+Bωcos(ωt))+1/C(Acos(ωt)+Bsin(ωt)) sin(ωt): 1: 0=-AωR+B/C cos(ωt): 2: u^ω=BωR+A/C nach Lösung des LGS: A=(Cωu^)/((RCω)^2+1), B=R((Cω)^2u^)/((RCω)^2+1) ip=Cωu^/((RCω)^2+1)cos(ωt)+(R(Cω)^2u^)/((RCω)^2+1)sin(ωt) -> i= ih+ip i=Ke^((-1/RC)t)+(Cωu^)/((RCω)^2+1)cos(ωt)+(R(Cω)^2u^)/((RCω)^2+1)sin(ωt) mit i(0)=(ua(0)-U0)/R -> K+(Cwu^)/((RCω)^2+1) K=-(U0/R+(Cωu^)/((RCω)^2+1) i=-e^((-1/RC))t(U0/R+(Cωu^)/((RCω)^2+1))+(Cωu^)/((RCω)^2+1)+(Cωu^)/((RCω)^2+1)cos(ωt)+(R(Cω)^2u^)/((RCω)^2+1)sin(ωt) für den Fall, dass U0=0: i=-Cωu^/((RCω)^2+1)e^(-1/(RC)t)+(Cωu^)/((RCω)^2+1)cos(ωt)+(R(Cω)^2u^)/((RCω)^2+1)sin(ωt) i=u^/((RCω)^2+1)(Cωcos(ωt)+R(Cω)^2sin(ωt)-Cωe^((-1/RC)t) d) ua=u^cos(ωt) (d(u^cos(ωt)))/dt=R(di/dt)+(1/C)i-u^ωsin(ωt)=R(di/dt)+(1/C)i partikuläre Lösung: ip=Acos(ωt)+Bsin(ωt) dip/dt=-Aωsin(ωt)+Bωcos(ωt) ip, dip/dt in DGL: -u^ωsin(ωt)=R(-Aωsin(ωt)+Bωcos(ωt))+1/C(Acos(ωt)+Bsin(ωt)) sin(ωt): 1: -u^ω=-AωR+B/C cos(ωt): 2: 0=BωR+A/C nach Lösung des LGS: A=(R(Cω)^2u^)/((RCω)^2+1) B=-(Cωu^)/((RCω)^2+1) ip=(R(Cω)^2u^)/((RCω)^2+1)cos(ωt)-(Cωu^)/((RCω)^2+1)sin(ωt)sin(ωt) i=ih+ip i=Ke^((-1/RC)t)+(R(Cω)^2u^)/((RCω)^2+1)cos(ωt)-(Cωu^)/((RCω)^2+1)sin(ωt) mit i(0)=(ua(0)-U0)/R->K+(R(Cw)^2u^)/((RCω)^2+1)=(u^cos(ω*0)-U0)/R K=(u^-U0)/R-(Cωu^)/((RCω)^2+1) i=e^((-1/RC)t)((u^-U0)/R-(Cωu^)/((RCω)^2+1)+(R(Cω)^2u^)/((RCω)^2+1)cos(ωt)-(Cωu^)/((RCω)^2+1)sin(ωt) i=e^((-1/RC)t)(u^/R-(Cωu^)/((RCω)^2+1))+(R(Cω)^2u^)/((RCω)^2+1)cos(ωt)-(Cωu^)/((RCω)^2+1)sin(ωt) |
| PDF Dokument Lösungen Differentialgleichungen |
Diese Seite wurde noch nicht kommentiert.





