Version [71757]
Dies ist eine alte Version von TutoriumMathe3L1 erstellt von Jorina Lossau am 2016-09-09 09:23:05.
Tutorium Mathematik 3
Anwendungen der Integralrechnung - Lösungen
| Aufgaben und Lösungen |
|---|
| 1) Eine Kette wird zwischen zwei gleich hohen Aufhänge punkten im Abstand l = 5 m befestigt. Gegenüber diesen Punkten hängt sie in der Mitte um d = 3 m durch. Wie lang ist die Kette? 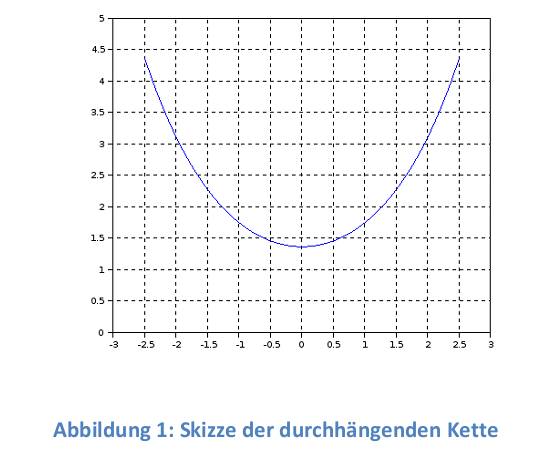 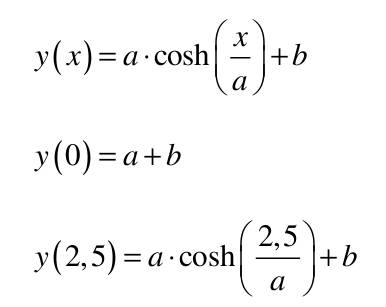 y(x)=a*cosh(x/a)+b y(0)=a+b y(2,5)=a*cosh(2,5/a)+b Die Kette hängt um d = 3m durch 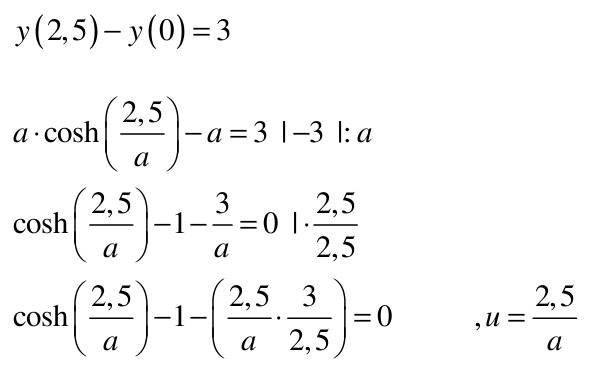 y(2,5)-y(0)=3 a*cosh(2,5/a)-1-(2,5/a)-1-3/a=0 I* 2,5/2,5 cosh(2,5/a)-1-(2,5/a*3/2,5)=0; u=2,5/a Nach der Substitution u = 2,5/a kann mit dem Newton-Verfahren die Nullstelle gesucht werden: 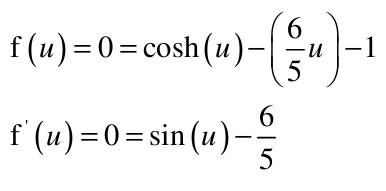 f(u)=0=cosh(u)-(6/5u)-1 f'(u)=0=sin(u)-6/5 Mit un=2 ergibt sich nach wenigen Iterationen u = 1,82937 und somit a = 2,5/u = 1,3666. Damit ist die Funktion, welche die Kettenlinie beschreibt eindeutig definiert und es kann die Bogenlänge berechnet werden. 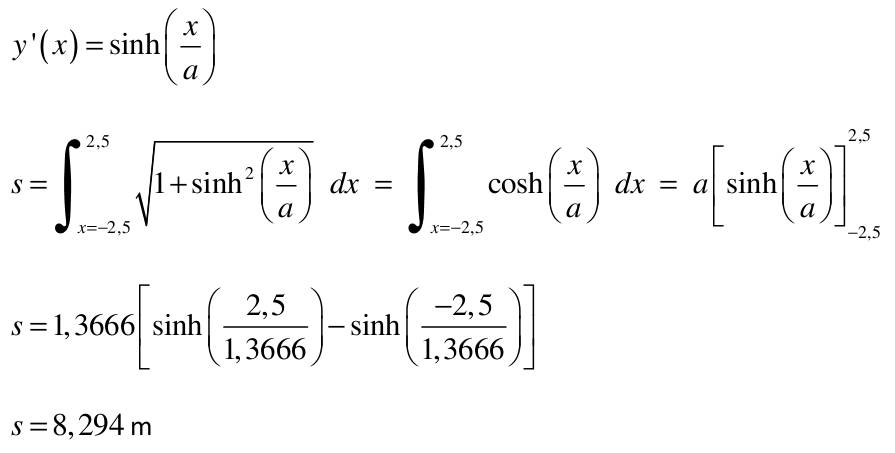 2) Ein Parabolspiegel wird durch die Rotation der Kurve y = k *x² um die y-Achse beschrieben. Wie groß ist seine Oberfläche für k = 1 / m = und 0 ≤ x ≤ 1 m (der Parabolspiegel hat also damit einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m).Vergleichen Sie die berechnete Oberfläche mit der einer Halbkugel vom Radius r = 1 m (Die Halbkugel hat auch einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m). mit k = 1 und y`(x) = 2x 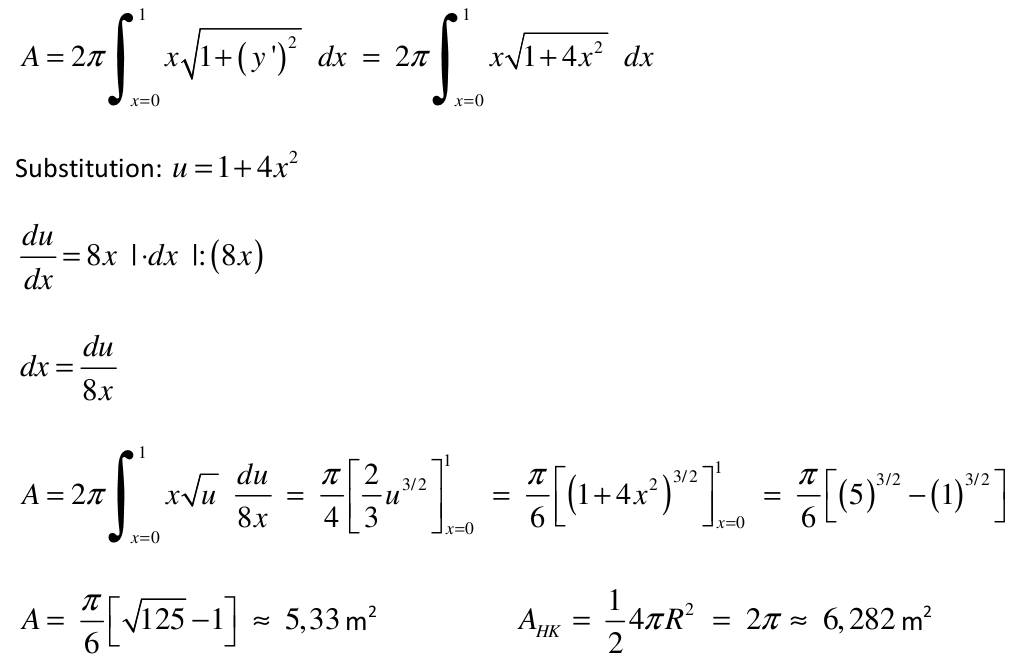 3) Während der Zeit T falle ein Strom gemäß einer e-Funktion vom Wert ˆi auf seine Hälfte. Berechnen Sie den integralen Mittelwert und den Effektivwert dieses Stroms in der Zeit T. 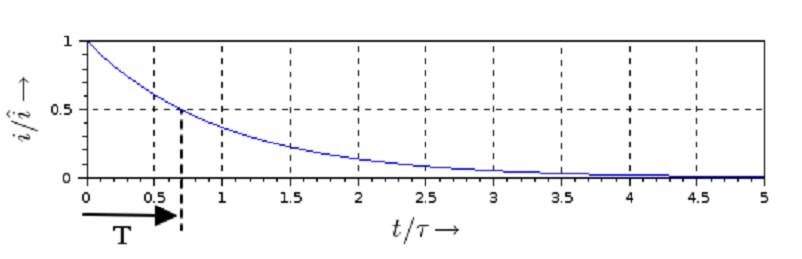 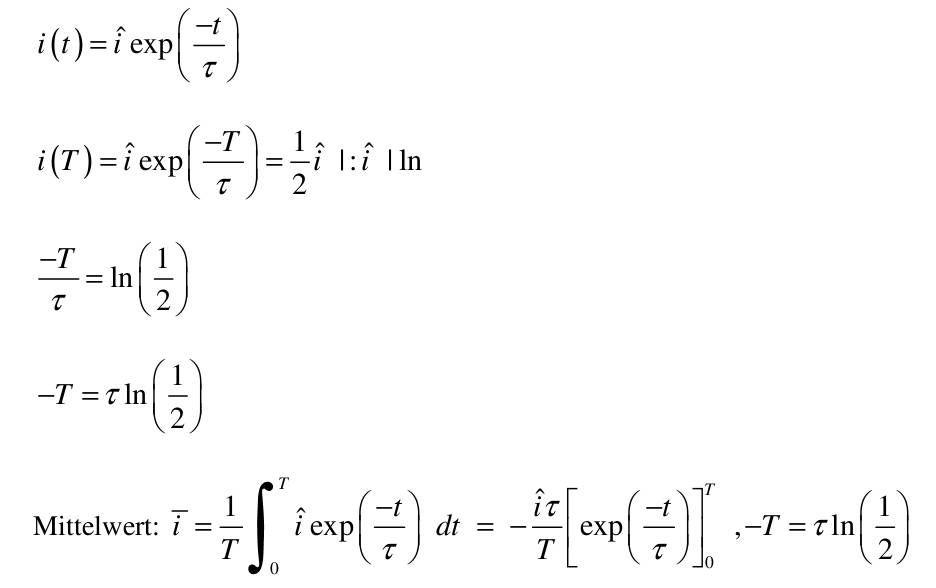 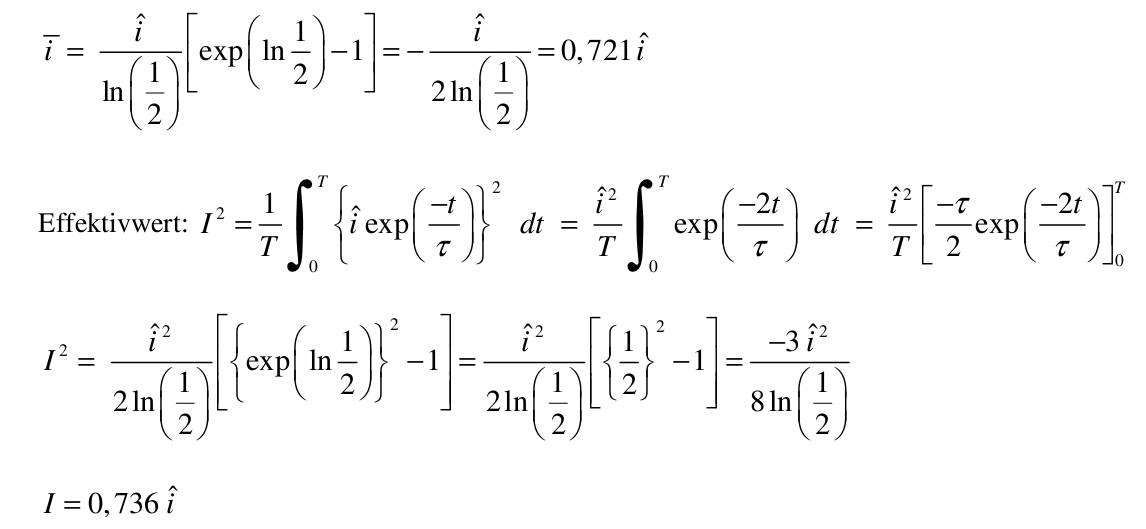 4) Ein Körper entsteht durch die Rotation der Kurve sin y Wurzel von x um die x-Achse, wobei gilt: 0 ≤ x ≤ π . Berechnen Sie das Volumen des Körpers. Hinweis: Verwenden Sie für das zu lösende Integral die partielle Integration, wobei Sie die Stammfunktion von sin²x aus dem Tabellenbuch entnehmen. 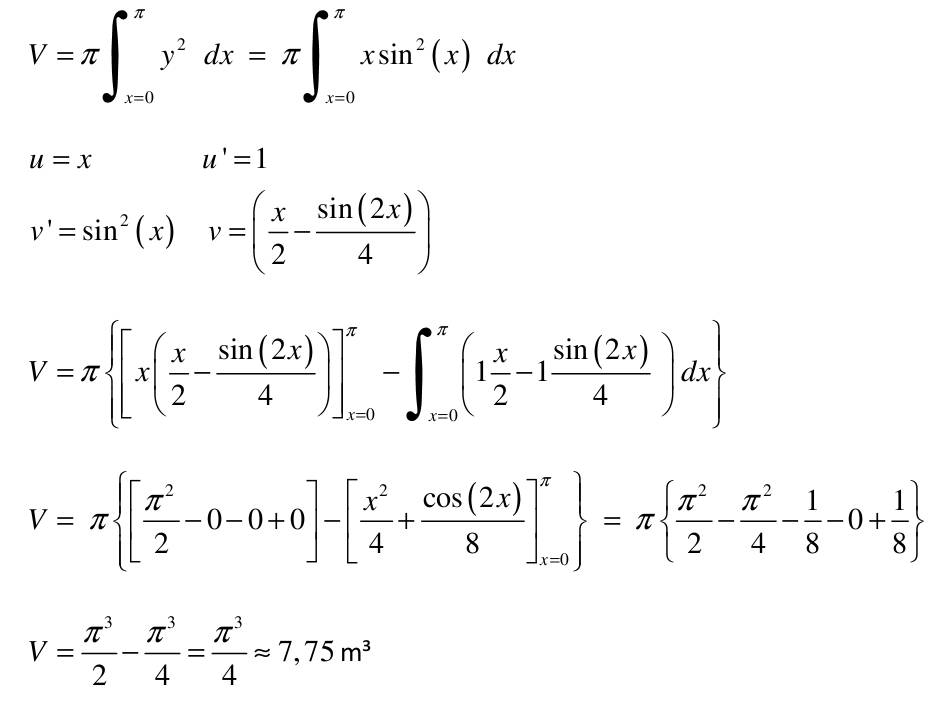 |
| PDF Dokument Lösungen Integralrechnung |
Diese Seite wurde noch nicht kommentiert.





