Tutorium Mathematik 3
Fourier - Reihen
Dirichletsche - Bedingungen: Eine stetige periodische Signalfunktion f(t) mit der Periodenlänge T lässt sich durch eine trigonometrische Reihe ausdrücken. Auch bei Vorliegen von endlich vielen Unstetigkeiten ist das möglich, sofern alle Unstetigkeiten Sprungstellen sind: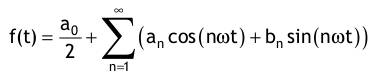 mit dem Gleichanteil: 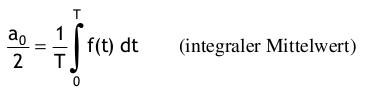 den Kosinusanteilen: 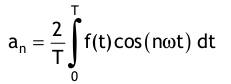 den Sinusanteilen: 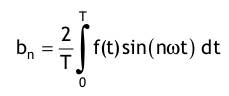 Anmerkungen:
Spezialfall: f(t) ist eine gerade Signalfunktion 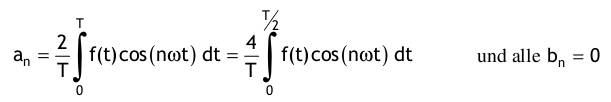 Spezialfall: f(t) ist eine ungerade Signalfunktion 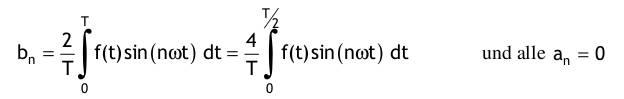 Reelle sin - Fourier - Reihe  Reelle cos - Fourier - Reihe 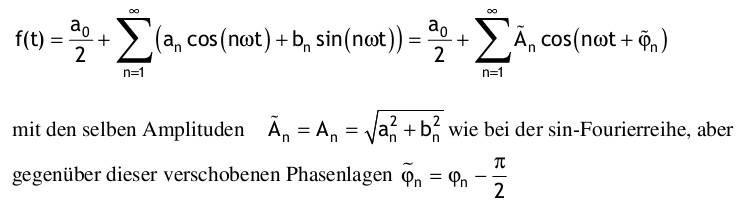 Komplexe Fourier - Reihe 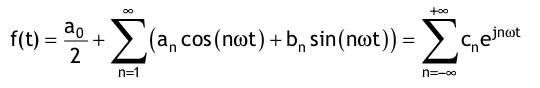 mit den komplexen Fourierkoeffizienten Cn, die sich entweder aus den reellen Fourierkoeffizienten berechnen lassen 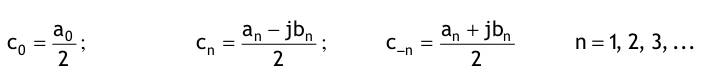 oder aus der gegebenen Signalfunktion: 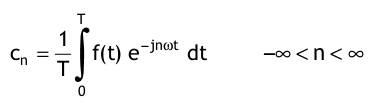 |
| PDF Dokument Fourier - Reihen |
Diese Seite wurde noch nicht kommentiert.





