Version [73395]
Dies ist eine alte Version von TutoriumMathe3A9 erstellt von Jorina Lossau am 2016-10-24 14:24:39.
Tutorium Mathematik 3
Laplace - Transformation - Aufgaben
| Aufgabe 2.1 Nachfolgend für t ≥ 0 definierte Funktionen haben für t < 0 den Funktionswert f(t) = 0. Transformieren Sie mit der Tabelle in den Bildbereich der Laplace-Transformation!  2.1.1. f(t)=4e^(-3t) 2.1.2. f(t)=1+2t+t^2 2.1.3. f(t)=(1+2t+t^2)e^(-2t) 2.1.4. f(t)=e^t+e^(-t) 2.1.5. f(t)=1/2(e^t-e^(-t)) 2.1.6. f(t)=sin(2t)+3cos(2t) 2.1.7. f(t)=e^(-4t)[sin(2t)+3cos(2t)] Aufgabe 2.2 Berechnen Sie die Bildfunktion unter Verwendung des Integrals, welches die Laplace-Transformation definiert.  2.2.1. f(t)= (0; t<0) (2; 0<t<2π) (2cos(3t), 2π<t) 2.2.2. f(t)= (0, t<0) (A, 0<t<3) (Ae^(-t-3), 3<t) Aufgabe 2.3 Transformieren Sie mit der Tabelle der Laplace-Korrespondenzen vom Bild- in den Zeitbereich. Falls nötig, zerlegen Sie die Ausdrücke zunächst in Partialbrüche. 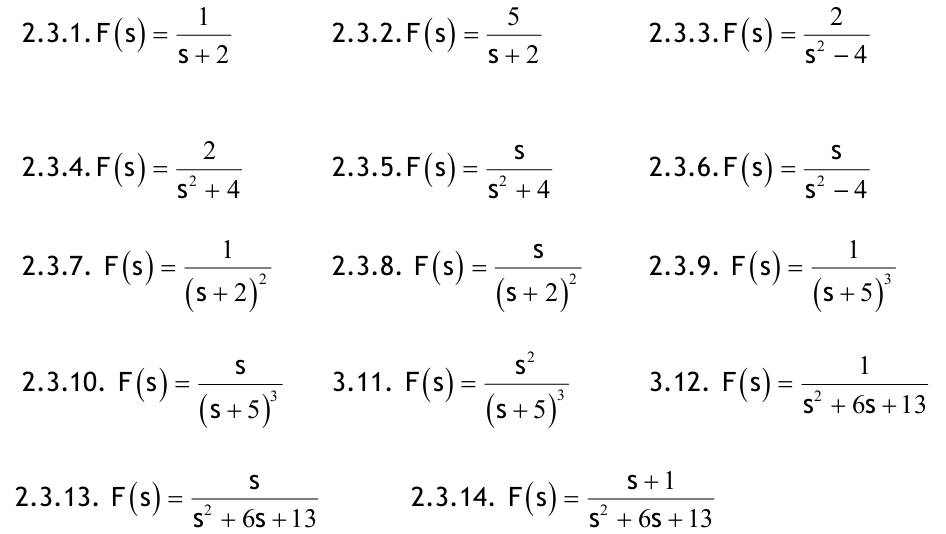 2.3.1. F(s)=1/(s+2) 2.3.2. F(s)=5/(s+2) 2.3.3. F(s)=2/(s^2-4) 2.3.4. F(s)=2/(s^2+4) 2.3.5. F(s)=s/(s^2+4) 2.3.6. F(s)=s/(s^2-4) 2.3.7. F(s)=1/(s+2)^2 2.3.8. F(s)=s/(s+2)^2 2.3.9. F(s)=1/(s+5)^3 2.3.10. F(s)=s/(s+5)^3 3.11. F(s)=s^2/(s+5)^3 3.12. F(s)=1/(s^2+6s+13) 2.3.13. F(s)=s/(s^2+6s+13) 2.3.14. F(s)=(s+1)/(s^2+6s+13) Aufgabe 2.4 Führen Sie die Partialbruchzerlegung durch und transformieren Sie danach in den Zeitbereich. 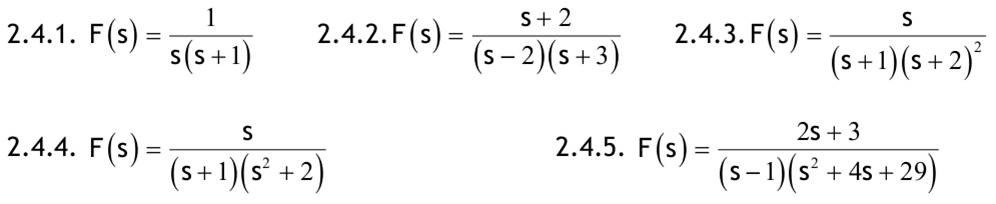 Aufgabe 2.5 Lösen Sie folgende Anfangswertaufgaben mit der Laplace-Transformation. 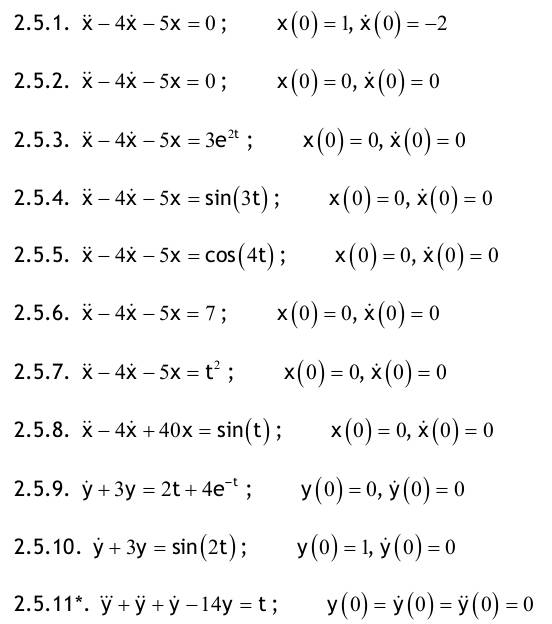 Aufgabe 2.6 Transformieren Sie in den Zeitbereich unter Verwendung der Faltungsregel!  |
| PDF Dokument Aufgaben Laplace - Transformation |
Diese Seite wurde noch nicht kommentiert.





