Version [70930]
Dies ist eine alte Version von TutoriumE3A2lsg erstellt von Jorina Lossau am 2016-08-10 14:34:36.
Tutorium Elektrotechnik 3
| File | Last modified | Size |
|---|---|---|
| schaltung1.jpg | 2023-10-06 18:37 | 9Kb |
| schaltung2.jpg | 2023-10-06 18:37 | 10Kb |
| schaltung3.jpg | 2023-10-06 18:37 | 12Kb |
| schaltung4.jpg | 2023-10-06 18:37 | 10Kb |
| tutorium_get_3_teil_2_loesungen.pdf | 2023-10-06 18:37 | 138Kb |
| tutorium_get_3_teil_2_loesungen_aufg_2.pdf | 2023-10-06 18:37 | 7Mb |
Ströme, Spannungen und Widerstände in RLC-Schaltungen
| 1.1 Beispielaufgabe Gegeben ist folgende Schaltung mit einer trigonometrischen Wechselspannungsquelle. 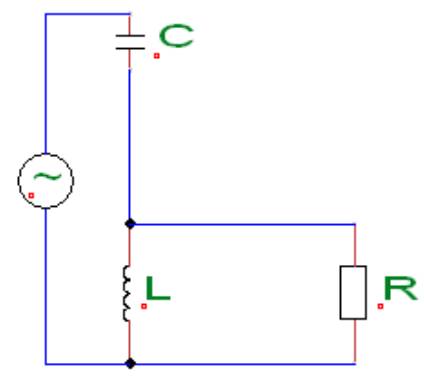 Die Bauteile haben folgende Kenndaten: R = 100Ω L = 1H C = 30µF f = 50 Hz u = 325 V a) Geben Sie u(t) als komplexes, imaginäres und reelles Zeitsignal an b) Geben Sie den Blindwiderstand XL an. c) Geben Sie den Blindleitwert BC an. d) Ermitteln Sie die komplexen Amplituden der Ströme iL, iR und iges mit Hilfe der komplexen Wechselstromrechnung e) Ermitteln Sie die komplexen Amplituden der Spannungen uC und uLR, mit Hilfe der komplexen Wechselstromrechnung. f) Geben Sie die Zeigerbilder der errechneten Ströme und Spannungen an. g) Geben Sie die Zeitsignale der errechneten Ströme und Spannungen an. Lösung: a) u(t) = u*(cos(2πft)+j* sin(2πft)) u(t) = 325V*(cos(2π*50Hz*t)+j*sin(2π*50Hz*t)) Re(u(t)) = 325V*cos(2π*50Hz*t) Im(u(t)) = 325V*sin(2π*50Hz*t) b) XL = wL = 2π* 50 Hz* 1H = 2π*50s^-1*1VsA^-1= 100πV/A=314,16Ω c) BC = wC = 2π* 50Hz* 30µF = 2π*50s^ -1*30*10^ -6AsV^ -1 = 9,425*10^ -3S d) YLR =1/R + 1/jwL = (jwL + R)/jwRL --> ZLR = jwRL/(jwL+R) ZC = 1/jwC Zges = 1/jwC + jwRL/(jwL + R) Erweiterung des zweiten Terms mit dem konjugiert Komplexen. Zges = 1/jwC+((jwRL/jwL+R)*(R-jwl/(R-jwL))) Zges = (w^2RL^2/(wL)^2+R^2)*j*((wR^2L)/(wL)^2+R^2)-j*1/wC=w^2RL^2/(wL)^2+R^2+j*((wR^2L/wLR+R^2))-1/wC) ReZges = ((2π*50)^2*100*1^2s^-2VA^-1V^2A^-2s1^2)/(2π*50*100s^-1VsA^-1)^2+(100VA^-1)^2 =90,8 Ω ImZges=(2π*50*100^2*1s^-1VsA^-1V^2A^-2)/(2π*50*1s^-1VsA^-1)^2+(100VA)^2-1/(2π*50*30*10^-6)s^-1AsV^-1 ImZges = -77,3Ω Z = √(Re² + Im²) = √(8244,64Ω² + 5959,84Ω² = 119,2Ω ℓ = arctan(Im/Re) = arctan(-77,2Ω/90,8Ω) =-40,37 Grad iges = u/Z = 325*e^(j*0^0V)/119,2*e^(-j*40,37GradVA^-1) = 2,73* e^(j*40,37Grad) A Errechnung der restlichen Ströme mit Hilfe der Stromteilerregel. iR/iges = YR/YLR = (1/R)/((1/R)+(1/jwL)) = jwL/(R+jwL) = (j*314,16Ω)/((100+j*314,16)Ω) iR = jwL/(R+jwL)*iges = ((314,16*e^(j*90Grad)Ω)/((329,69*e^(j*72,34Grad)Ω)*2,73*e^j*40,37Grad A = 314,16Ω/329,69Ω*2,73A iR = (314,16Ω/329,69Ω)*2,73A*e^(j*(90Grad+40,37Grad-72,34Grad)) = 2,6*e^(j*58,03Grad)A iL = YL/YLR*iges = R/(R+jwL)*iges = (100*e^(j*0Grad)Ω)/((329,69*e^(j*72,43Grad)Ω))*2,73*e^(j*40,37Grad)A iL = 0,83*e^(-j*31,91Grad)A uC = ZC*iC = 106,1*e^(-j*90Grad)VA^ -1*2,73*e^(j*40,37Grad) A = 289,65*e^(-j*49,63Grad)V uC = 289,65(cos(-49,63Grad)+j*sin(-49,63Grad))V = (137,63+j*215,82)V uLR = u - uC = (325 - 187,37 + j* 215,82)V = (137,63 + j*215,82)V uLR = 255,97* e^(j*57,47Grad) uLR = iLR/YLR = iLR/(1/R+1/jwL) = (2,73*e^(j*40,37Grad)A)/(0,0105*e^(-j*17,64Grad)AV^-1) = 260*e^(j*58,01Grad)V g) u(t) = u*e^jwt = u*e^(jwt+ℓ) uc(t) =289,65*e^j*(100ℓπs^-1*t-49,63Grad)V 1.2 Aufgabe 1 Gegeben ist die abgebildete Schaltung: 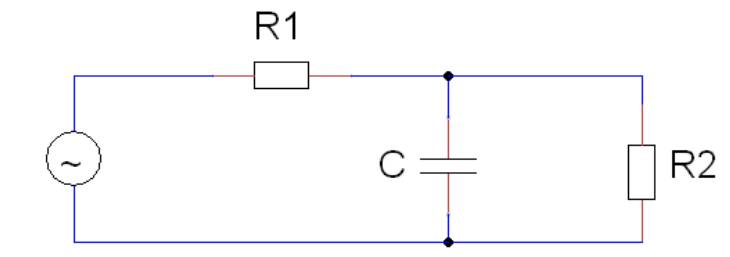 Die Bauteile haben folgende Kenndaten: R1 = 1kΩ R2 = 1kΩ C = 1µF f = 120 Hz iR2 = 8mA Berechnen Sie den Strom IC durch den Kondensator und die Spannung U0. Lösung: Als erstes muss man die Spannung ermitteln, die über den Kondensator abfällt. uR2=uC=R2*iR2=1000VA^-1*8*10^-3A=8V Danach wird der komplexe Widerstand des Kondensators ermittelt. ZC=1/jwC=-j*1326,29Ω*e^-(j*90Grad) Mithilfe des ohmschen Gesetzes lässt sich iC berechnen. iC=uC/ZC=8V/(1326,29VA^-1*e^(-j*90Grad))=6mA*e^(-j*90Grad) Die Gesamtspannung U0 lässt sich mithilfe der Spannungsteilerregel ermitteln. u0/UC=(R1+1/(1/R2+jwC))/(1/(1/R2+jwC))=R1/R2+1+jwR1C u0=(R1/R2+1+jwR1C)*UC u0=(2+0,7540j)*8V=(16+6,0319j)V=17,10V*e^(j*20,66Grad) 1.3 Aufgabe 2 Gegeben ist die abgebildete Schaltung. 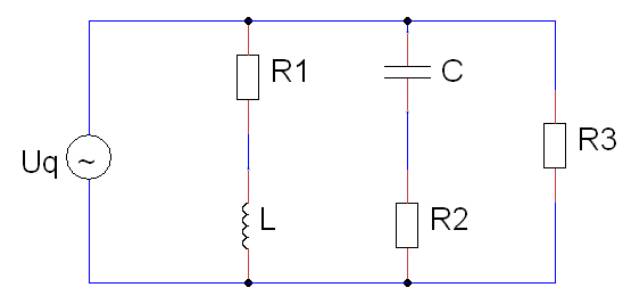 R1 = 10Ω R2 = 20Ω R3 = 10Ω L = 10 mH C = 100µF f = 50 Hz u = 10 V Berechnen Sie den Gesamtstrom der in der Schaltung mit Hilfe der Zeigerbilder.(Hinweis: Teilen Sie die Schaltung in einzelne Abschnitte ein.) 1.4 Aufgabe 3 Eine RLC-Schaltung liegt an einer Spannungsquelle mit trigonometrischen Spannungsverlauf. Gegeben sind: R = 3kΩ L = 0,5 H C = 62,5nF u = 35,355354V w = 4000s^-1 a) Wie groß ist der Effektivwert Ueff? b) Geben Sie die Impedanz ZLC an. c) Wie groß ist der komplexe Gesamtstrom? d) Wie lautet der zeitliche Verlauf i(t) des Gesamtstromes? e) Zeigt die Schaltung ein kapazitives oder ein induktives Verhalten auf? Lösung: a) U=u/√2=25V b) ZLC=j*4kΩ c) Z=ZR+ZLC=(3+4j)kΩ Z=5kΩ*e^(j*53,13Grad) I=25V/(5000VA^-1*e^(j*53,13Grad) d)i=√2*I=707mA*e^(-j*53,13Grad) i(t)=707mA*e^(j*(4000s^-1-53,13Grad)) i(t)=Re{i(t)}=707mA*cos(4000s^-1-53,13Grad) e) Die Schaltung zeigt ein induktives Verhalten, weil der Winkel der komplexen Stromamplitude negativ ist. 1.5. Quellen Leonhard Stiny: Aufgaben mit Lösungen zur Elektrotechnik : 350 Übungsaufgaben zur Elektrotechnik mit ausführlichen Musterlösungen. 2. Auflage, Poing: Franzis Verlag GmbH, 2008 |
| PDF Dokument Lösungen Teil 2 |
| PDF Dokument Lösungen Teil 2 Aufgabe 2 |
Diese Seite wurde noch nicht kommentiert.





