Version [33667]
Dies ist eine alte Version von SkriptPhysikZweiWellenMaschbau erstellt von JulianOsthues am 2013-08-13 13:01:25.
| HINWEIS: Das hier Angebotene Skript kann in keinen Fall den Gang zur Vorlesung ersetzen! Es dient lediglich zur Veranschaulichung und soll weitere Hinweise und Erläuterungen zu wichtigen Thematiken geben. |
1. Wellen
1. Eindimensionale Wellen:
| Defintion Welle: Eine Welle ist eine räumliche Ausbreitung eines Schwingungszustandes |
Merke: Eine Welle ist eine zeitliche und räumliche Änderung einer physikalischen Größe
Es gibt zwei Möglichkeiten Eindimensionaler Wellen sich auszubreiten:
- 1. Transversalwelle: Schwingungsrichtung senkrecht zur Ausbreitungsrichtung
(z. B.: elektromagnetische Wellen, Wasserwellen oder auch Schallwellen in Festkörpern)
- 2. Longitudinalwelle: Schwingungsrichtung parallel zur Ausbreitungsrichtung
(z. B.: Schallwellen in Gasen sowie in Gasen, in manchen Fällen auch in Festkörpern)
Zum Zeitpunkt t=0 stellen sich folgende Wellen ein:
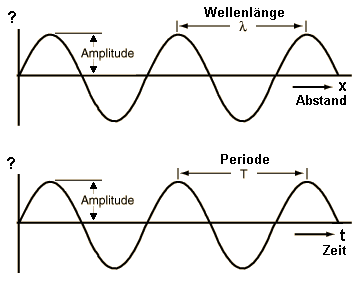
[Abbildung 1]
Aus der bereits aus dem ersten Semester bekannten Formel Geschwindigkeit = Strecke/Zeit also, v = s/t können wir auf den Zusammenhang zwischen der Ausbreitungsgeschwindigkeit c, Wellenlänge λ und der Periode T schließen.
So ergibt sich für die Ausbreitungsgeschwindigkeit c:
c = λ / T bzw. c = λ* f
wobei die Frequenz f das Reziproke (=der Kehrwert) der Periode T, also f = 1/T ist.
1. Beispiel Berechnung der Wellenlänge einer Schallwelle:
λ = c/f
λ = 340 m*s/435 s
λ =0.78 m
Phase: Die Phase einer Welle gibt an, in welchem Abschnitt innerhalb einer Periode sich die Welle zu einem Referenzzeitpunkt und -ort befindet. Sie legt also fest, wie groß die Auslenkung ist.
Wellenfront: 3 Dimensionale Fläche, die alle Punkte gleicher Phase miteinander verbindet.
Die Wellenfront kann ich sich in zwei Arten (bei einer 1-dimensionalen Welle) ausbreiten. Sie bilden sich aufgrund des Huygenschen Prinzipes wie folgt aus:
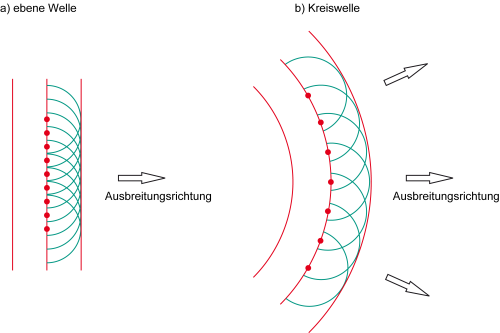
[Abbildung 2]
Verwendete Quellen:
- Vorlesungsmitschrift von Prof. Dr. Udo Behn
Verwendete Grafiken:
- Abbildung 2: http://psi.physik.kit.edu/img/Ausbreitung.png
Diese Seite wurde noch nicht kommentiert.





