Version [62895]
Dies ist eine alte Version von MatheGKL6 erstellt von Jorina Lossau am 2015-12-15 11:00:45.
Tutorium Mathematischer Grundkurs
| File | Last modified | Size |
|---|---|---|
| MatheGKL6.pdf | 2023-10-06 18:37 | 42Kb |
| MatheGKL61.jpg | 2023-10-06 18:37 | 65Kb |
| MatheGKL62.jpg | 2023-10-06 18:37 | 73Kb |
| MatheGKL63.jpg | 2023-10-06 18:37 | 111Kb |
| MatheGKL64.jpg | 2023-10-06 18:37 | 38Kb |
| vektoren1.jpg | 2023-10-06 18:37 | 12Kb |
| vektoren2.jpg | 2023-10-06 18:37 | 2Kb |
| vektoren3.jpg | 2023-10-06 18:37 | 8Kb |
| vektoren4.jpg | 2023-10-06 18:37 | 13Kb |
| vektoren5.jpg | 2023-10-06 18:37 | 19Kb |
| vektoren6.jpg | 2023-10-06 18:37 | 11Kb |
Vektoren - Lösungen
| 6. Schwerpunkt Grundlagen der Vektorrechnung 0.6.1.T In einem Punkt greifen 4 Kräfte an, wobei F1=500N nach Norden, F2=300N nach Westen und F3=400N nach Süden zieht. Wie groß muß die nach Osten gerichtete Kraft F4sein, damit die resultierende Kraft F Rgenau nach Nordosten zeigt? Welchen Betrag hat dann FR? Lösung: 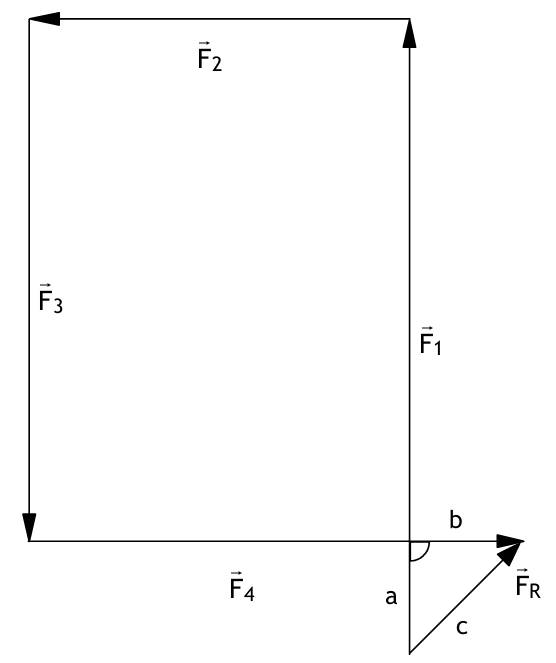  1cm = 50 N F1 + F2 + F3 + F4 = FR N =^ y; 0=^ x (0 500) + (-300 0) + (0 -400) + (x 0) = (a a) -300 + x = a 100 = a x = a + 300 = 400 F4 = (400 0) FR = (a a) (100 100) IFRI = 100*√2N = 141,4 N 0.6.2.T Die Punkte A (1,1,1) B (-1,5,3) C (-4,-3,-3) bestimmen ein Dreieck. Skizze: 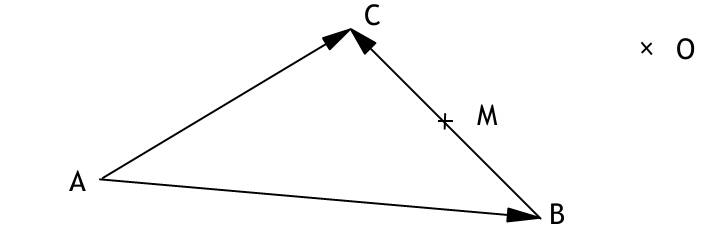 a) Berechnen Sie den Umfang dieses Dreiecks. AB = OB - OA = (-1 5 3) - (1 1 1) = (-2 4 2) IABI = √((-2)² + 4² + 2²) = 2√6 BC = (-3 -8 -6) BC = √((-3)² + (-8)² + (-6)²) = √109 CA = √(5² + 4² + 4²) = √57 u = IABI + IBCI + ICAI ≈ 22,89 LE b) Geben Sie den Vektor von A zum Mittelpunkt M der Seite BC an. AM = AB + 1/2 BC = (-2 4 2) + 1/2(-3 -8 -6) 0 (-3,5 0 -1) c) Geben Sie den Ortsvektor zum Punkt M an OM = OA + AM = (1 1 1) + (-3,5 0 -1) = (-2,5 1 0) d) Geben Sie einen Vektor an, der den Innenwinkel in Punkt A halbiert 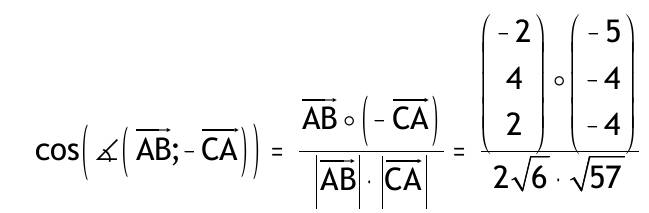 = (10-16-8)/6√38 = -0,37857 AB;-CA = 112,24° 0.6.3.T a) Finden Sie die Menge aller Vektoren c, die zu a und b orthogonal sind. b) Bestimmen sie einen Einheitsvektor ec, der zu a und b orthogonal ist. a = (1 0 2) b = (0 2 1) 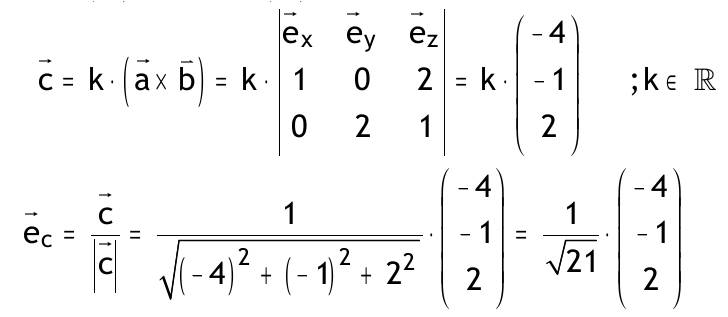 0.6.4.T Finden Sie einen Punkt D, so dass er zusammen mit den Punkten A, B, C ein Parallelogramm bildet. A (1,2,5); B(-1,4,7); C(5,6,9). Berechnen Sie den Umfang des Parallelogramms und geben Sie die Diagonalvektoren an. Bedingung für Parallelogramm : gegenüberliegende Seiten vektorgleich; es gibt genau 3 Möglichkeiten das Dreieck zum Parallelogramm zu ergänzen. eine Möglichkeit : AB = CD OB - OA = OD - OC OD = OB - OA + OC (x y z) = (-1 4 7) - (2 3 5) + (5 6 9) = (2 7 11) = OD D(2,7,11) Umfang: AB = CD = BD u = 2* IABI + 2* IACI = 2*√((-3)² + 1² + 2²) + 2*√(3² + 3² + 4²) = 19,15 LE AB = (-3 1 2) AC = (3 3 4) Diagonalvektoren: AD = AB + BD = AB + AC = (0 4 6) BC = BD - CD = AC - AB = (6 2 2) Skizze: 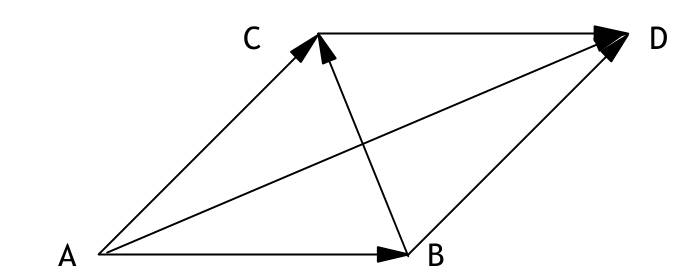 |
| PDF Dokument Lösungen Vektoren |
Diese Seite wurde noch nicht kommentiert.





