Version [65909]
Dies ist eine alte Version von LoesungenDBR erstellt von Jorina Lossau am 2016-03-06 18:54:54.
Tutorium Kostenrechnung
Problemlösungen DBR - Lösungen
| Wiederholung Differenzen-Quotienten-Verfahren Beispiel: In der Fertigungsstelle II eines Betriebes mit einer Periodenkapazität von 1.000 Arbeitsstunden werden einheitliche Rohlinge gefräst. Von den beiden letzten Abrechnungsperioden liegen folgende Angaben vor: PI: 79 % Kapazitätsauslastung, 4.740 Stück, 130.800 € Gesamtkosten PII: 85 % Kapazitätsauslastung, x Stück, 138.000 € Gesamtkosten Für die Periode III wurde eine Auslastung von 75 % geplant. Ermitteln Sie die Gesamtkosten für die Planperiode III. 79 % = 4.740 Stück = 130.800 € 85 % = 5.100 Stück = 138.000 € Diff. = 360 Stück = 7.200 € kv = 7.200 / 360 = 20 € Kf = K – Kv = 130.800 – 20*4.740 = 36.000 75 % = 4.500 Stück K = 36000 + 4.500 * 20 = 126.000 Zusatzaufträge Zusatzaufträge sind Aufträge, die ein Unternehmen annimmt, sofern es kapazitätsmäßig nicht ausgelastet ist. Die Frage, ob Zusatzaufträge angenommen werden sollen, lässt sich nur mit Hilfe der Deckungsbeitragsrechnung beantworten. Beispiel: Ein Unternehmen fertigt zwei Produkte. Für den laufenden Monat gelten folgende Daten: variable Kosten: 80 €/Stück Fixe Kosten: 100.000 €/Monat Erlös: 220 €/Stück Absatzmenge: 800 Stück/Monat Fertigungskapazität: 1.400 Stück/Monat Es besteht die Möglichkeit, 200 weitere Produkte zum Preis von 180 €/Stück abzusetzen. Erfolg ohne Zusatzauftrag: Erlös: 800 * 220 = 176.000 - Kv: 800 * 80 = 64.000 = DB: 800 * (220-80) = 112.000 - Kf: 100.000 = Gewinn: 12.000 Erfolg mit Zusatzauftrag: Erlös: 800 * 220 + 200 * 180 = 212.000 - Kv: 1.000 * 80 = 80.000 = DB: 132.000 - Kf: 100.000 = Gewinn: 32.000 Kürzerer Lösungsweg: Vergleicht man lediglich die variablen Kosten und den Erlös durch den Zusatzauftrag, kann die Vorteilhaftigkeit, also der Beitrag zur Deckung der Fixkosten, des Zusatzauftrages ermittelt werden. zusätzlicher DB = (p-kv)*x = (180 – 80) * 200 = 20.000 zusätzlicher DB = E-Kv = 180 * 200 – 80 * 200 = 20.000 Übung: Ein Einproduktunternehmen, das über eine Kapazität von 40.000 Stück/Monat verfügt, arbeitet mit einem Beschäftigungsgrad von 50 %. Die fixen Kosten betragen 100.000 €/Monat, die variablen Kosten 60.000 €/Monat. Der Verkaufspreis liegt bei 10,00 €/Stück. Es besteht nun die Möglichkeit, im Rahmen eines Exportauftrages einmalig weitere 10.000 Stück des Erzeugnisses zu Preis von 5,00 €/Stück abzusetzen. Würden Sie die Annahme dieses Zusatzauftrages befürworten? Begründen Sie ihre Antwort rechnerisch. … Kürzerer Lösungsweg:... |
| Eigenerstellung vs. Fremdbezug Das Problem Eigenerstellung/Fremdbezug bezieht sich auf den Produktionsbereich eines Unternehmens. Es stellt sich die Frage, ob es günstiger ist Produkte (bspw. Zulieferteile) selbst zu erstellen oder von einem externen Unternehmen zu beziehen. Kurzfristige Optimierung Eigenfertigung, wenn die variablen Kosten niedriger sind als der Preis des Zulieferers Die fixen Kosten werden nicht berücksichtigt, da sie kurzfristig unabhängig davon anfallen, ob eigengefertigt oder fremdbezogen wird. |
| Maschine A | Lieferant | |
| Kapazität | 12.000 | |
| Fertigungs-/Absatzmenge | 10.000 | |
| Variable Kosten/Stück | 14,50 | 0,00 |
| Fixe Kosten/Stück | 7,20 | 0,00 |
| Beschaffungspreis | 0,00 | 12,30 |
| Verkaufspreis | 32,50 | 32,50 |
| Bezogen auf die kurzfristige Optimierung ist es zu empfehlen, die Erzeugnisse fremd zu beziehen, da der Beschaffungspreis um 2,20 €/Stück unter den variablen Kosten liegt. Langfristige Optimierung Bei der Überlegung, ob langfristig Eigenerstellung oder Fremdbezug günstiger ist, wird davon ausgegangen, dass die Produktionsausstattung veränderbar ist. D. h. die Fixkosten sind Bestandteil der Überlegung. Vorheriges Beispiel: Bezogen auf die langfristige Optimierung ist es zu empfehlen, die Erzeugnisse fremd zu beschaffen, da die gesamten Stückkosten um 9,40 €/Stück über dem Preis des Zulieferers liegen. Hier wird davon ausgegangen, dass die fixen Kosten abbaubar oder noch gar nicht entstanden sind. |
| Rentabilität einer Werbeaktion Bei der Frage, ob sich eine Werbeaktion lohnt, werden die Kosten der Werbeaktion in ein Verhältnis mit dem Stückdeckungsbeitrag des zu bewerbenden Produkts gesetzt. Hierdurch wird die nötige Absatzsteigerung ermittelt, mit der die Kosten der Werbeaktion gedeckt und eventuell ein zusätzlicher Gewinn erzielt wird. Beispiel: Fixkosten 50.000 €, variable Stückkosten 10 €, Stückpreis 15 €. Eine einmalige Werbeaktion erfordert Kosten in Höhe von 20.000 €. Wie viel Stück müssen einmalig zusätzlich gefertigt und abgesetzt werden, um allein die Werbungskosten wieder hereinzubringen? alter BEP = 50.000 / 5 = 10.000 Stück zusätzliche Menge = zusätzliche Kosten / db = 20.000 / 5 = 4.000 Stück neuer BEP = bisherige Kf + zusätzliche Kosten) / db = 70.000 / 5 = 14.000 Stück Welche gesamte Absatz- und Umsatzsteigerung müsste die Werbeaktion bewirken, wenn der Gewinn um 10.000 € pro Jahr verbessert werden soll? Werbungskosten: 20.000 + Gewinnsteigerung: 10.000 = notwendiger DB: 30.000 notwendige Absatzsteigerung = notwendiger DB / db = 30.000 / 5 = 6.000 Stück notwendige Umsatzsteigerung = 6.000 Stück * 15 = 90.000 € |
| Break-Even-Point-Analyse Ermittlung der Gewinnschwellenmenge und des –umsatzes Beispiel: Ein Unternehmer hat in der vergangenen Periode Fixkosten in Höhe von 50.000 € und proportionale Stückkosten von 10 €. Es wurden nur Aufträge angenommen, die einen Festpreis von 15 € erbrachten. Die Produktion betrug dadurch 14.000 Stück, was einer Kapazitätsauslastung von 70 % entspricht. Bei welcher Ausbringungsmenge liegt die Gewinnschwelle? |
| Produktion in Stück | Kf | Kv | Kf | Kv | E | e | Db | db |
| 2.000 | 50.000 | 20.000 | 25,00 | 10 | 30.000 | 15 | 10.000 | 5 |
| 4.000 | 50.000 | 40.000 | 12,50 | 10 | 60.000 | 15 | 20.000 | 5 |
| 6.000 | 50.000 | 60.000 | 8,33 | 10 | 90.000 | 15 | 30.000 | 5 |
| 8.000 | 50.000 | 80.000 | 6,25 | 10 | 120.000 | 15 | 40.000 | 5 |
| 10.000 | 50.000 | 100.000 | 5,00 | 10 | 150.000 | 15 | 50.000 | 5 |
| 12.000 | 50.000 | 120.000 | 4,17 | 10 | 180.000 | 15 | 60.000 | 5 |
| 14.000 | 50.000 | 140.000 | 3,57 | 10 | 210.000 | 15 | 70.000 | 5 |
| Der Umsatz der Gewinnschwelle reicht gerade aus, um mit der Summe der hier erlösten Stückdeckungsbeiträge die Fixkosten auszugleichen. Die Produktion jedes weiteren Stücks führt zu einem Gewinn in Höhe des vollen db. Die Gewinnschwelle ist die Ausbringungsmenge, bei der die Summe der Erlöse gleich der Summe der Kosten ist. (Break-even-Point) BEP = Kf/db BEP = 50.000 / 5 = 10.000 Stück Grafische Betrachtung des BEP: 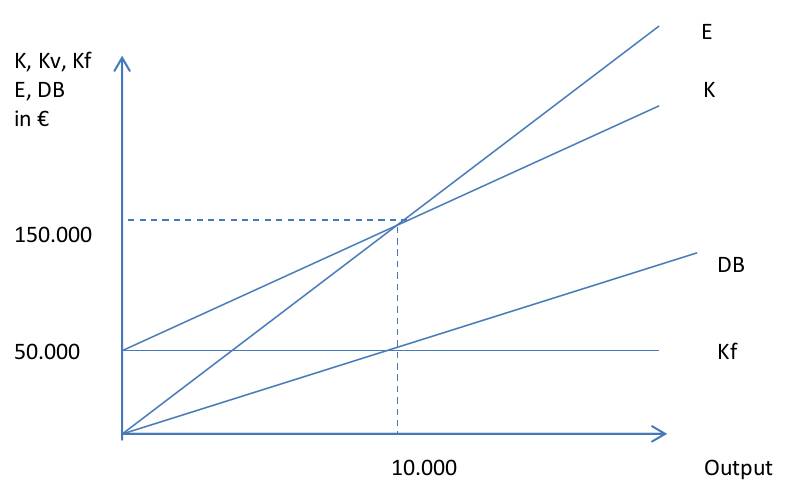 |
| Bestimmung des optimalen Produktionsprogrammes Durchführung - Feststellung eines Produktionsengpasses - Bestimmung des relativen Deckungsbeitrages -> db/Einheit
- Beachtung eventueller Lieferverpflichtungen - Produktion nach Rangfolge bis zur Kapazitätsausschöpfung |
| Übungen 1. Ein Unternehmen stellt bislang nur das Produkt A her. Die Einzelkosten betragen 30,00 €/Stück. Die Gemeinkosten bei einer maximalen Ausbringungsmenge von 5.000 Stück betragen 200.000,00 €, davon sind 25 % variabel. Die Erlöse belaufen sich bei einem Beschäftigungsgrad von 70 % auf 350.000 €. a) Für den kommenden Monat Oktober liegen Bestellungen in Höhe von 2.000 Stück des Produkts A vor. Berechnen Sie die Höhe der ungedeckten Fixkosten bei dieser Ausbringungsmenge. b) Der Kunde K wäre außerdem zur Abnahme einer größeren Stückzahl von A bereit, wenn ihm ein Sonderrabatt von 10 % eingeräumt würde. Ermitteln Sie die zusätzliche Stückzahl, die Kunde K bestellen müsste, damit die Gewinnschwelle im Monat Oktober erreicht wird. c) Begründen Sie, warum die Unternehmensleitung einen zusätzlichen Auftrag von K annehmen sollte, wenn dieser weniger als die unter Frage 3 ermittelte Stückzahl bestellen sollte. d) Durch Rationalisierungsmaßnahmen können die Fixkosten um 25 % abgebaut werden und die variablen Kosten um 5,00 €/Stück reduziert werden. Ermitteln Sie das Betriebsergebnis bei einer Ausbringungsmenge von 2.200 Stück. 2. In einem Industriebetrieb wurden für Produkt S in der Abrechnungsperiode I bei einer Produktionsmenge von 3.000 Stück (= Beschäftigungsgrad 37,50 %) Gesamtkosten von 75.000 € ermittelt. In der Abrechnungsperiode II betrugen bei einem Beschäftigungsgrad von 75 % die fixen Stückkosten 10 €. In beiden Perioden belief sich die Gewinnschwellenmenge auf 5.000 Stück. 2.1 Berechnen Sie die fixen Gesamtkosten, die variablen Stückkosten und den Stückverkaufspreis von Produkt S. 2.2 Die variablen Stückkosten werden in der Abrechnungsperiode III auf 6,00 € erhöht. 2.2.1 Berechnen Sie den neuen Break-Even-Umsatz für die Abrechnungsperiode III. 2.2.2 Mit Produkt S soll nun in der Abrechnungsperiode III ein Betriebsgewinn von 5.000 € erzielt werden. Dies ist allerdings nur erreichbar, wenn eine einmalige zusätzliche Werbeaktion mit Kosten in Höhe von 11.500 € durchgeführt und der Preis um 1,00 €/Stück gesenkt wird. Ermitteln Sie, wie hoch der Absatz von Produkt S sein müsste, um diesen Gewinn zu erzielen. 2.2.3 Berechnen Sie die langfristige Preisuntergrenze in der Abrechnungsperiode III bei einer Absatzmenge von 7.500 Stück, wenn die Werbeaktion nicht durchgeführt wird. 3. Die Auslastung eines Betriebes mit einer maximalen Kapazität von 6.000 Stück von Produkt P konnte im Vergleich zum Vormonat von 60 % auf 75 % gesteigert werden. Dadurch entstanden zusätzliche Kosten in Höhe von 20.700 €. In der laufenden Periode betragen die Gesamtkosten 135.500 €. 3.1 Ermitteln Sie rechnerisch die Fixkosten 3.2 Stellen Sie die Kostenfunktion auf. 3.3 Berechnen Sie die Stückkosten bei einem Beschäftigungsgrad von 80 % und den BEP, wenn ein Stück für 31 € verkauft wird. |
| Lösung 1. a) Kf = 200.000 * 0,75 = 150.000 kv = 30 + 50.000 / 5.000 = 40 (EK sind zu 100 % variabel, GK zu 25 %) Output bei 70 % Beschäftigungsgrad = 5.000 * 0,7 = 3.500 Stück p = 350.000 / 3.500 = 100 NVE 200.000 (100 * 2.000) - Kv 80.000 (40 * 2.000) = DB 120.000 ((100 – 40)*2.000) - Kf 150.000 = BE - 30.000 b) neuer p = 100 * 0,9 = 90 30.000 / (90 – 40) = 600 Stück c) Der Zusatzauftrag trägt mit einem db von 50,00 € zur Deckung der fixen Kosten bei. d) neue Kf = 150.000 * 0,75 = 112.500 neue kv = 40 – 5 = 35 NVE 220.000 - Kv 77.000 = DB 143.000 - Kf 112.500 = BE 30.500 2.1 3.000 = 37,5 % -> 6.000 = 75 % Kf = 6.000 * 10 = 60.000 Kv = K – Kf -> 75.000 – 60.000 = 15.000 kv = Kv / x = 15.000 / 3.000 = 5 5.000 = 60.000 / db -> db = 12 p = db + kv -> 5 + 12 = 17 2.2.1 BEP = 60.000 / 11 = 5.455 Stück BEU (Break-even-Umsatz) = 5.455 * 17 = 92.735 2.2.2 (60.000 + 5.000 + 11.500) / (16-6) = 7.650 Stück 2.2.3 langfr. PU = kv + kf -> 12 + 60.000/7.500 = 14 € 3.1 3.600 Stück = 114.800 € 4.600 Stück = 135.500 € Diff. 900 Stück = 20.700 € kv = 20.700 / 900 = 23 € Kf = K – Kv = 114.800 - 3.600 * 23 = 32.000 3.2 K = 32.000 + 23x 3.3 80 % = 4.800 Stück 32.000 / 4.800 + 23 = 29,67 €/Stück BEP = 32.000 / (31-23) = 4.000 Stück |
Diese Seite wurde noch nicht kommentiert.





