Version [65709]
Dies ist eine alte Version von DBR erstellt von Jorina Lossau am 2016-03-03 12:32:06.
Tutorium Kostenrechnung
Deckungsbeitragsrechnung - Lösungen
| Unterschied zwischen Vollkosten- und Teilkostenrechnung Ein in Aussicht gestellter Kundenauftrag für Produkt P mit einem Preislimit von 35.000,00 € soll durch die Betriebsbuchhaltung geprüft werden ob er angenommen werden soll oder nicht. An Kosten fallen an: Einzelkosten (variable Kosten): Fertigungsmaterial 9.000 €, Fertigungslöhne 8.000 € Es wird mit folgenden Zuschlagsätzen gerechnet: MGK 10 %, FGK 200 %, VwVtGK 10 %. Dabei beträgt der Fixkostenanteil der Gemeinkosten: MGK 80 %, FGK 40 %, VwVtGK 60 %. Ermitteln Sie den Gewinn/Verlust nach der Vollkostenrechnung sowie den Deckungsbeitrag nach der Teilkostenrechnung. Vollkostenrechnung: FM: 9.000 MGK 10%: 900 FL: 8.000 FGK 200%: 16.000 HK: 33.900 VwVtGK 10%: 3.390 SK: 37.290 Erlöse: 35.000 Umsatzergebnis/Verlus: -2.290 Teilkostenrechnung: Erlöse: 35.000 -variable Kosten:... FM: 9.000 MGK: 900*0,2 oder (9.000* 0,1* (1-0,8)) = 180 FL: 8.000 FGK: 16.000* 0,6 oder (8.000*2*(1-0,4)) = 9.600 VwVtGK: (3.390*(1-0,6)) = 1.356 =Deckungsbeitrag: 6.864 |
| Ergebnis: Obwohl die Vollkostenrechnung einen Verlust aufweist, wird – bei ausreichender Kapazität – der Auftrag nach der marktorientierten Teilkostenrechnung angenommen, da der positive Deckungsbeitrag, der erwirtschaftet wird, zur Deckung der ohnehin anfallenden fixen Kosten beiträgt. Langfristig muss natürlich Vollkostendeckung und darüber hinaus ein angemessener Gewinn gefordert werden. Die Teilkostenrechnung (Deckungsbeitragsrechnung) bietet Entscheidungshilfen für Zusatzaufträge, Preisuntergrenze, Eigenfertigung vs. Fremdbezug, Gewinnschwellenmenge (Break Even Point), Kosten einer Werbeaktion, Planung des optimalen Produktionsprogramms. Einstufige DBR Bei der einstufigen DBR, auch Direct Costing genannt, wird mit einem einzigen Fixkostenblock gearbeitet. Bei ihr ergibt sich folgender Deckungsbeitrag (DB): DB = Erlöse – Variable Kosten = E – Kv = E – kv*x Beispiel für Einproduktunternehmen Eine Unternehmung produziert genau ein Produkt. Die variablen Kosten der betrachteten Periode liegen bei insgesamt 180.000 €. Der Listenverkaufspreis beträgt 1.250 € und die gesamten Fixkosten 240.000 €. Ermitteln Sie das Betriebsergebnis bei einem Output von 500 Stück. Erlöse (p*x): 625.000 -Kv: 180.000 =DB: 445.000 -Kf: 240.000 =BE: 205.000 1. Gewinnschwellen-Analyse Die Gewinnschwellenmenge ist die Menge, bei der alle Kosten gedeckt werden. Jede zusätzliche verkaufte Einheit stellt eine Erhöhung des Unternehmensgewinns dar. Bei linearem Gesamtkostenverlauf, gleichbleibenden fixen Kosten und konstanten Preisen ergibt sich die Gewinnschwelle bzw. der Break-even-Point grafisch: 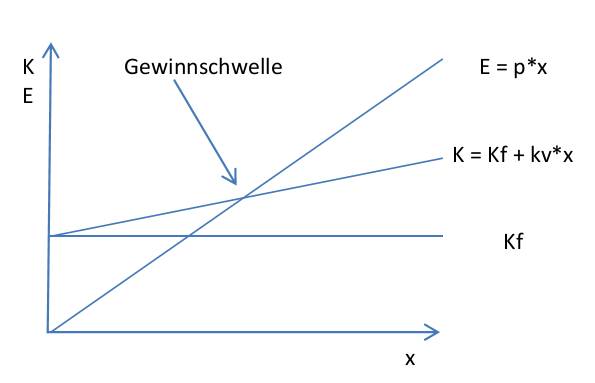 Rechnerische Ermittlung der Gewinnschwellenmenge` Bedingung: DB = Kf oder E = K ->db * x = Kf ->x = Kf/db ->Kf + kv*x = p*x ->db ist der Stückdeckungsbeitrag, also p – kv Beispiel: Ein Unternehmen produziert ein Produkt bei 52,50 € variablen Kosten pro Stück und fixen Kosten in Höhe von 312.000 €. Der Preis für das Produkt beträgt 114,90 €. Gewinnschwelle: 312.000/ (114,90 – 52,50) = 5.000 Stück |
| Ermittlung des Betriebsergebnisses für Einproduktunternehmen Beispiel: Ein Unternehmen stellt bislang nur das Produkt A her. Die Einzelkosten betragen 30 €/Stück. Die Gemeinkosten bei einer maximalen Ausbringungsmenge von 5.000 Stück betragen 200.000 €, davon sind 25 % variabel. Die Erlöse belaufen sich bei einem Beschäftigungsgrad von 70 % auf 350.000 €. Für den Monat Oktober liegen Bestellungen in Höhe von 2.000 Stück des Produkts vor. Berechnen Sie die Höhe der ungedeckten Fixkosten bei dieser Ausbringungsmenge. … Nettoverkaufserlöse (NVE = p*x):200.000 = 100 * 2.000 -Kv: 80.000 = 40 * 2.000 = DB [=(p-kv)*x]: 120.000 = (100-40)*2000 -Kf: 150.000 = Betriebsergebnis (BE): - 30.000 |
| Mehrstufige DBR Bei der mehrstufigen DBR wird nicht mit einem einzigen Fixkostenblock gearbeitet, sondern die fixen Kosten den Erzeugnissen und Gruppen von Erzeugnissen zugeordnet. Der Teil der fixen Kosten, der sich nicht zuordnen lässt, heißt Fixkostenrest. Dieser Rest entspricht den unternehmensbezogenen Fixkosten. DB = Erlöse – variable Kosten – verschiedene Fixkosten Analyse der Fixkosten: a)ErzeugnisfFixkosten (dem einzelnen Erzeugnis zurechenbar z. B. Kosten für Maschinen) b) Unternehmensfixkosten (betreffen alle Erzeugnisse gemeinsam z. B. Kosten für Verwaltung) |
| Ermittlung des Betriebsergebnisses für Mehrproduktunternehmen Beispiel: Ein Unternehmen der chemischen Industrie stellt Messstreifen für Umweltgifte her. Zurzeit werden drei Messstreifen (A, B und C) produziert. Die Messstreifen stellen unterschiedliche Gifte fest und müssen aus technischen Gründen auf verschiedenen Anlagen in getrennten Werkhallen produziert werden. Für die Lagerhaltung wird eine gemeinsame Lagerhalle genutzt, Vertrieb und Verwaltung sind in einem Gebäude konzentriert und werden vom gleichen Personal durchgeführt. Von der Kostenrechnung werden für den vergangenen Monat folgende Werte ermittelt. Die Unternehmensfixkosten betragen 15.200 €. Wie hoch ist das Betriebsergebnis? |
| Artikel | A | B | C |
| Stückpreis in € | 9,90 | 15,50 | 12,65 |
| variable Kosten/Stück in € | 4,90 | 7,30 | 7,50 |
| verkaufte Stückzahl | 8.000 | 10.000 | 4.000 |
| Erzeugnisfixkosten in € | 30.000 | 40.000 | 20.400 |
| Produkt A | Produkt B | Produkt C | Gesamt | |
| Erlöse | 79.200 | 155.000 | 50.600 | 281.800 |
| - Kv | 39.200 | 73.000 | 30.000 | 142.000 |
| = DB I | 40.000 | 82.000 | 20.600 | 139.600 |
| - erz. Kf | 30.000 | 40.000 | 20.400 | 90.400 |
| = DB II | 10.000 | 42.000 | 200 | 52.200 |
| - unt. Kf | -15.200 | |||
| = BE | 37.000 |
| Mit Hilfe der mehrstufigen DBR lassen sich die Kosten differenzierter berechnen und Entscheidungen über Förderung und die Einstellung von Produkten besser treffen. DB I zeigt an, welcher Betrag für jede Produktgruppe zur Deckung der jeweiligen Erzeugnisfixkosten zur Verfügung steht. DB II gibt an, inwiefern Vollkostendeckung aller zurechenbaren Kosten erreicht wird bzw. welcher Beitrag zum Betriebsergebnis geleistet wird. Ein negativer DB II liegt bei einem Produkt dann vor, wenn es seine Erzeugnisfixkosten nicht mehr vollständig abdecken kann. Im Hinblick auf die Gewinnoptimierung besteht die Möglichkeit, die Einstellung der Fertigung eines eventuellen Verlustartikels zu überprüfen. |
| Die Deckungsbeitragsrechnung in der Stückbetrachtung Beispiel: Kostenträger eines Zulieferbetriebs sind einheitliche Rohlinge, bei deren Verarbeitung für Material, Löhne, Energie etc. 10,00 €/Stück an proportionalen Kosten anfallen. Die Kunden A, B und C benötigen jeweils 500 Stück und sind bereit je Stück 15 €, 10 € bzw. 9 € zu zahlen. Welche Aufträge werden bei freier Fertigungskapazität angenommen? p: (Preis) Nettoerlös je Stück - kv: variable Kosten je Stück = db: Deckungsbeitrag je Stück |
| Kunde | A | B | C |
| Berechnung des db: p-kv = db | 15,00-10,00=5,00 | 10,00-10,00=0 | 9,00-10,00=-1,00 |
| Entscheidungshilfe | db ist positiv Hier sind die variablen Kosten voll durch den Preis abgedeckt und jedes Stück trägt zudem zur Deckung der fixen Kosten bei. ->Annahme des Auftrags | db =Null Es sind nur die variablen Kosten von dem erzielten Preis abgedeckt. Die kurzfristige Preisuntergrenze ist damit erreicht. ->Annahme des Auftrags | db ist negativ Hier sind nicht mal die variablen Kosten ganz abgedeckt. Jedes produzierte Stück würde den Verlust um 1,00 € erhöhen. ->Ablehnung des Auftrags |
| Im Zulieferbetrieb betragen die fixen Kosten 40.000 € pro Monat bei einer Kapazität von 6.250 Stück. Der Markt lässt langfristig nur einen Beschäftigungsgrad von 80 % zu. Berechnen Sie die langfristige Preisuntergrenze (Vollkostendeckung: Kf + Kv). langfr. PU = 40.000 / 6.250 * 0,8 + 10 = 18 € Unterscheidung zwischen langfristiger und kurzfristiger Preisuntergrenze Die kurzfristige Preisuntergrenze deckt lediglich die varibalen, nicht aber die fixen Kosten ab. Sie dient als Entscheidungsgrundlage, ob Zusatzaufträge bei freier Kapazität angenommen werden sollen. Die langfristige Preisuntergrenze deckt sowohl die variablen als auch die fixen Kosten ab. Sie erfüllt somit die Bedingung der Vollkostendeckung. Der Deckungsbeitragssatz (DBS) auf der Grundlage des db Er gibt Auskunft, wie viel Prozent des Erlöses zur Deckung der Fixkosten zur Verfügung stehen. Je höher der %-Satz, desto größer ist die Wahrscheinlichkeit der Deckung der Fixkosten und der Gewinnerzielung. |
| A | B | |
| DBS = db * 100 / p | 5*100/15=33,33% | 0 * 100 / 10 = 0 % |
| Ãœbungen zur Deckungsbeitragsrechnung 1. Ein Unternehmen kann jährlich 8.000 Stück eines Erzeugnisses produzieren, lastet seine Kapazität aber nur zu 60 % aus. Die Erzeugnisse werden zum Preis von 35 €/Stück verkauft. Die fixen Kosten liegen bei 50.000 € pro Jahr, die variablen Kosten betragen 15 €/Stück. Die Geschäftsleitung ist an einer verbesserten Auslastung der Kapazität interessiert und beauftragt ein Marktforschungsinstitut mit der Erstellung einer Marktanalyse. Darin zeigt sich, dass voraussichtlich 1.200 Stück pro Jahr mehr abgesetzt werden könnten, wenn der Preis der Erzeugnisse um 3 €/Stück gesenkt würde. Wie verändert sich der Stückdeckungsbeitrag bei Erhöhung der Produktion? Wie verändert sich die Gewinnschwelle bei Erhöhung der Produktion? Welche Auswirkungen hat die Erhöhung der Produktion auf Umsatz, Deckungsbeitrag und Gewinn? 2. Es werden drei Produkte hergestellt. Die gesamten Fixkosten betragen 450.300 €. Davon können 25 % Produkt A zugerechnet werden. Fixkosten in Höhe von 27.300 € sind keinem Produkt zuzuordnen. Produkt B bringt einen negativen DBII von 24.135 €. Das Betriebsergebnis beträgt 112.600 €. Berechnen Sie für den Monat die fehlenden DB I und DB II sowie die Erzeugnisfixkosten. Folgende Daten liegen für einen Monat vor: |
| A | B | C | |
| Preis pro Stück in € | 362,00 | 540,00 | |
| variable Kosten pro Stück in € | 200,00 | 340,00 | |
| Ausbringungsmenge | 1.200 | 1.000 | 950 |
| 3. Ãœber die Produktion des Artikels X sind aus der Vorperiode folgende Werte bekannt: proportionale Stückkosten 100 € Stückpreis 400 € a) Ermitteln Sie den Deckungsbeitragssatz. b) Durch einen Preisanstieg beim Fertigungsmaterial und eine Tarifanhebung bei den Fertigungslöhnen erhöhen sich die direkten Stückkosten so, dass sich nur noch ein DBS von 55 % errechnet. Ermitteln Sie den künftigen Wert der proportionalen Stückkosten. c) Der Anstieg der proportionalen Kosten soll teilweise durch eine Preisanhebung so aufgefangen werden, dass zumindest ein DBS von 60 % erreicht wird. Berechnen Sie die notwendige Höhe des Stückpreises. 4. Ein Unternehmen fertigt nur das Produkt Y im Kapazitätsrahmen von 2.000 Stück/Periode. Errechnet sind die Periodenfixkosten mit 72.000 € und die proportionalen Stückkosten mit 40 €. Zudem wurde bislang der Stückdeckungsbeitrag mit 60 € unterstellt. a) Bei welchem Beschäftigungsgrad (in %) wird die Gewinnschwelle erreicht? b) Ermitteln Sie den Deckungsbeitragssatz. 5. Bei einem Output von 15.000 Stück eines Produktes entstehen Gesamtkosten in Höhe von 650.000 €, davon sind 450.000 € produktionsbedingt. a) Ermitteln Sie die absolute (kurzfristige) Preisuntergrenze für die Annahme von Aufträgen d) Berechnen Sie die langfristige Preisuntergrenze. |
Lösung
| bei 4.800 Stück pro Jahr | bei 6.000 Stück pro Jahr | |
| Preis | 35 | 32 |
| - variable Kosten | 15 | 15 |
| =DB | 20 | 17 |
| Gewinnschwelle= Kf/db | 50.000/20 = 2.500 | 50.000/17 = 2.941 |
| bei 4.800 Stück pro Jahr | bei 6.000 Stück pro Jahr | |
| Erlöse (Umsatz) | 168.000 | 192.000 |
| - variable Kosten | 72.000 | 90.000 |
| =DB | 96.000 | 102.000 |
| - fixe Kosten | 50.000 | 50.000 |
| = Gewinn | 46.000 | 52.000 |
| Produkt A | Produkt B | Produkt C | Gesamt | |
| NVE | 434.400 | 513.000 | ||
| - Kv | 240.000 | 323.000 | ||
| = DB I | 194.400 | 178.500 | 190.000 | |
| - erz. Kf | 112.575 | 202.635 | 107.790 | 423.000 |
| = DB II | 81.825 | - 24.135 | 82.210 * | 139.900 |
| - unt. Kf | 27.300 | |||
| = BE | 112.600 |
| * * 139.900 = 81.825 – 24.135 + x x = DB II von C 3. a) 400 – 100 = 300 -> 300 * 100 / 400 = 75 % b) db = 55 * 400 / 100 = 220 Euro -> p – db = kv -> kv = 400 – 220 = 180 Euro 4. Kf/db = 72.000 / 60 = 1.200 Stück 2.000 Stück entsprechen 100 %, 1.200 entsprechen folglich 60 %. DBS = db*100/p = 60*100/100 = 60 % 5. kurzfr. PU = Kv/x = 450.000 / 15.000 = 30 Euro langfr. PU = K/x = 650.000 / 15.000 = 43,34 Euro (aufrunden, da sonst ein kleiner Verlust entsteht) |
| PDF Dokument Lösungen Teil 1 |
| PDF Dokument Lösungen Teil 2 |
| File | Last modified | Size |
|---|---|---|
| Übungen zur Deckungsbeitragsrechnung.docx | 2023-10-06 18:36 | 26Kb |
| 1.1 Lösung Deckungsbeitragsrechnung.docx | 2023-10-06 18:36 | 36Kb |
| DBL1.pdf | 2023-10-06 18:36 | 257Kb |
| DBL2.pdf | 2023-10-06 18:36 | 332Kb |
| DBR.jpg | 2023-10-06 18:36 | 14Kb |
Diese Seite wurde noch nicht kommentiert.





