Wissensdatenbank Wirtschaftsrecht: TutoriumMathe3L8

1.6 Lösen Sie die folgenden Differentialgleichungenmit der Methode der „Variation der Konstanten“.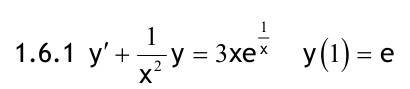 zug. hom.: 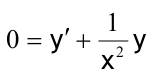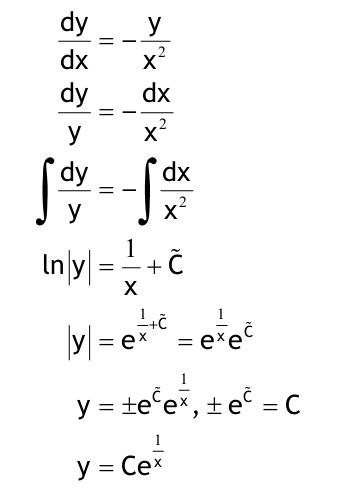Variation der Konst.: 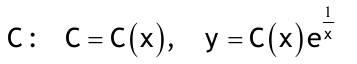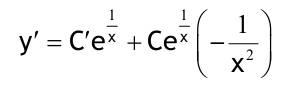in DGL: 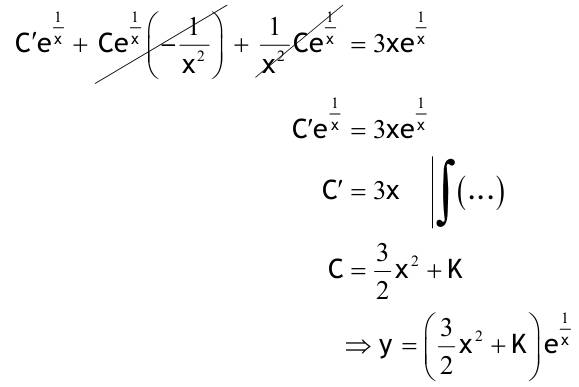= allgemeine Lösung 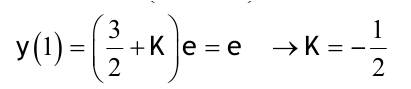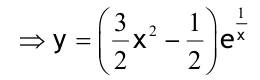= spezielle Lösung 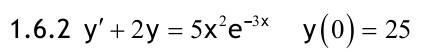zug. hom.: y' + 2y = 0 char. Gleichung: 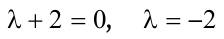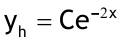Variation der Konst.: 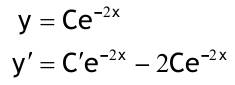in inhom. DGL: 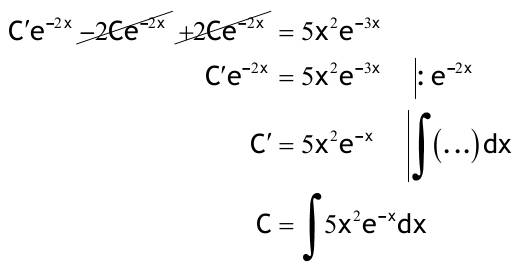mit part. Integration: 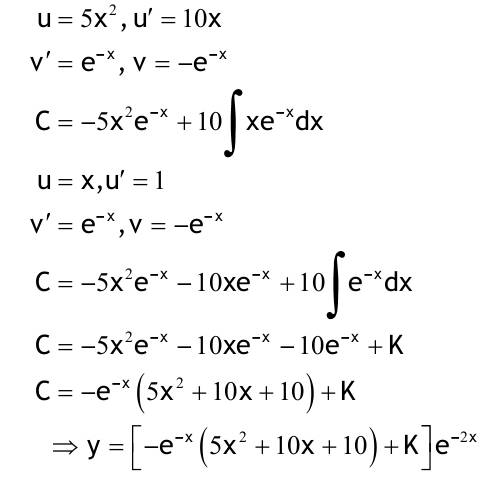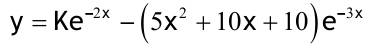= allgemeine Lösung y(0) = 25 25 = K - 10 --> K = 35 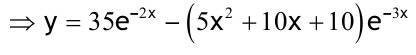= spezielle Lösung 1.6.3 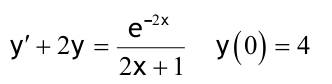zug. hom.: y' +2y = 0 charakt. Gl.: 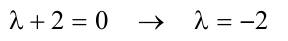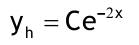Var. d. Konst.: 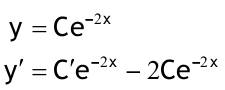in DGL: 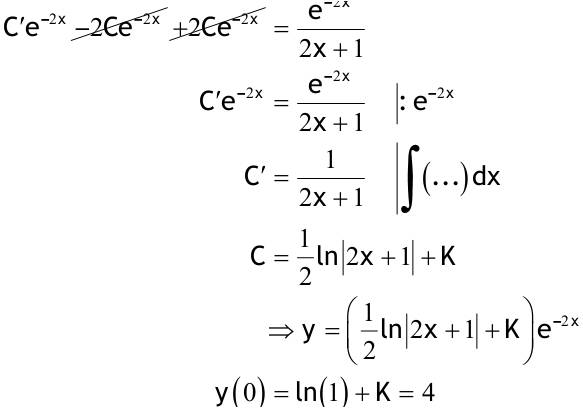K = 4 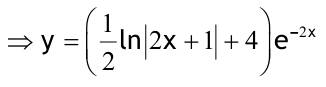= spezielle Lösung 1.6.4 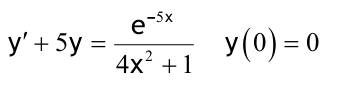zug. hom.: y' + 5y = 0 charakt. Gl.: 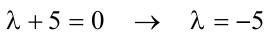Var. der Konst.: 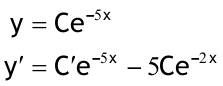in DGL: 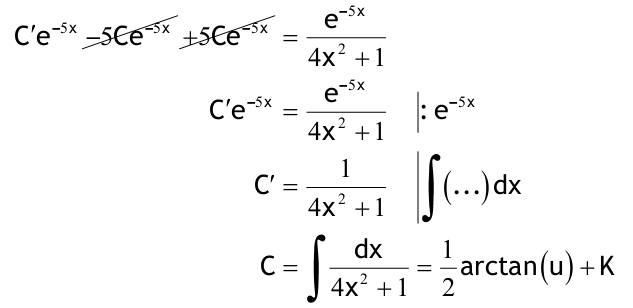lin. Substitution: 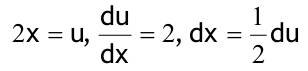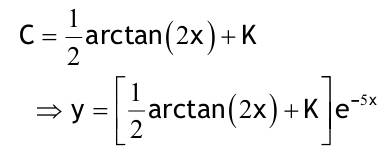= allgemeine Lösung y(0) = K = 0 = spezielle Lösung 1.6.5 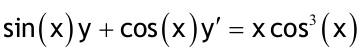y(0) = -2 zug. hom.: sin(x)y + cos(x)y' = 0 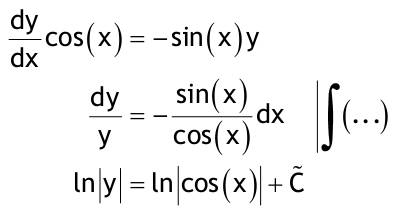Var. d. Konst.: C ist nun Funktion von x y = Ccos(x) y'=C'cos(x)-Csin(x) in DGL: 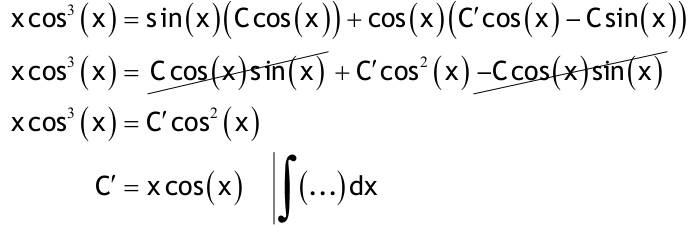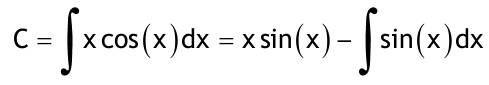u = x, u' = 1 v' = cos(x), v = sin(x) C = xsin(x) + cos(x) + K --> y = (xsin(x) + cos(x) + K) cosx) = allgemeine Lösung y(0) = 1 + K = -2 K = -3 --> y = (xsin(x) + cos(x) -3) cos(x) = spezielle Lösung 1.6.6 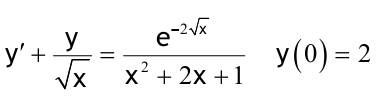zug. hom.: 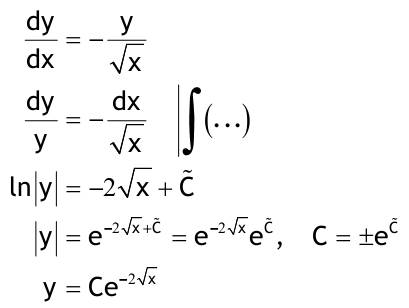Var. d. Konst.: C ist nun eine Funktion von x 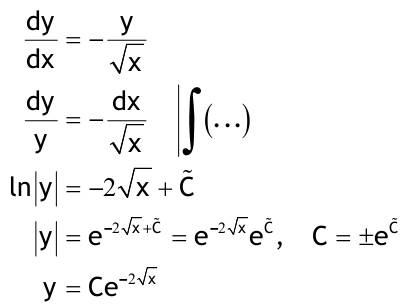in DGL: 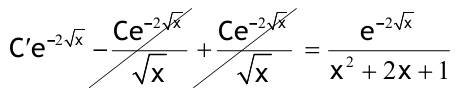= allgemeine Lösung y(0) = K - 1 = 2 --> K = 3 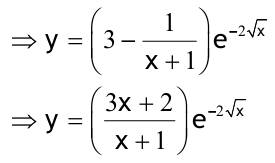= spezielle Lösung