Version [58415]
Dies ist eine alte Version von TutoriumMathe3L1 erstellt von Jorina Lossau am 2015-08-28 18:58:21.
Tutorium Mathematik 3
| File | Last modified | Size |
|---|---|---|
| Integralrechnung1.jpg | 2023-10-06 18:37 | 10Kb |
| Integralrechnung2.jpg | 2023-10-06 18:37 | 18Kb |
| Integralrechnung3.jpg | 2023-10-06 18:37 | 7Kb |
| Integralrechnung4.jpg | 2023-10-06 18:37 | 26Kb |
| Integralrechnung5.jpg | 2023-10-06 18:37 | 38Kb |
| Integralrechnung6.jpg | 2023-10-06 18:37 | 18Kb |
| Integralrechnung7.jpg | 2023-10-06 18:37 | 26Kb |
| Integralrechnung8.jpg | 2023-10-06 18:37 | 40Kb |
| Integralrechnung9.jpg | 2023-10-06 18:37 | 39Kb |
| Mathe3L1.pdf | 2023-10-06 18:37 | 77Kb |
| Mathe3L11.jpg | 2023-10-06 18:37 | 42Kb |
| Mathe3L12.jpg | 2023-10-06 18:37 | 40Kb |
| Mathe3L13.jpg | 2023-10-06 18:37 | 42Kb |
| Mathe3L14.jpg | 2023-10-06 18:37 | 63Kb |
| Mathe3L15.jpg | 2023-10-06 18:37 | 82Kb |
| Mathe3L16.jpg | 2023-10-06 18:37 | 53Kb |
| Skizze.jpg | 2023-10-06 18:37 | 35Kb |
Anwendungen der Integralrechnung - Lösungen
| Aufgaben und Lösungen |
|---|
| 1) Eine Kette wird zwischen zwei gleich hohen Aufhänge punkten im Abstand l = 5 m befestigt. Gegenüber diesen Punkten hängt sie in der Mitte um d = 3 m durch. Wie lang ist die Kette? 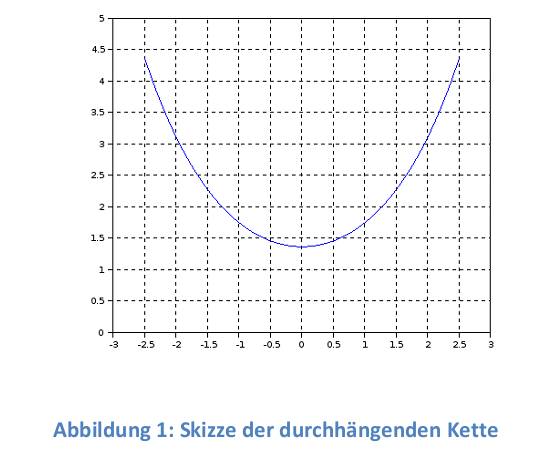 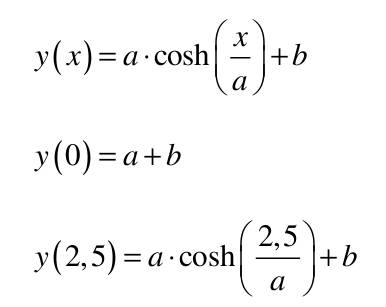 Die Kette hängt um d = 3m durch 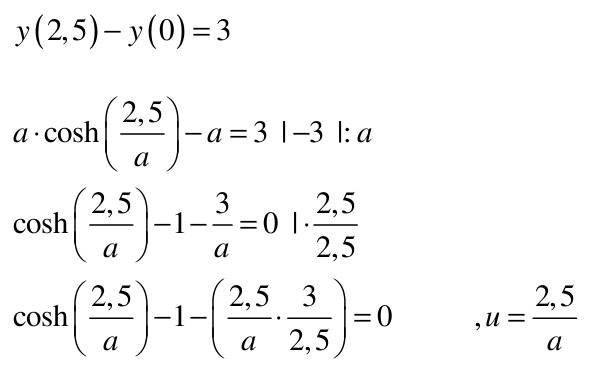 Nach der Substitution u = 2,5/a kann mit dem Newton-Verfahren die Nullstelle gesucht werden: 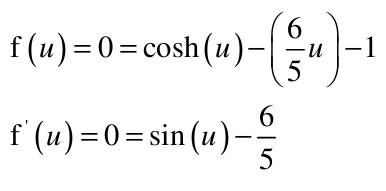 Mit un=2 ergibt sich nach wenigen Iterationen u = 1,82937 und somit a = 2,5/u = 1,3666. Damit ist die Funktion, welche die Kettenlinie beschreibt eindeutig definiert und es kann die Bogenlänge berechnet werden. 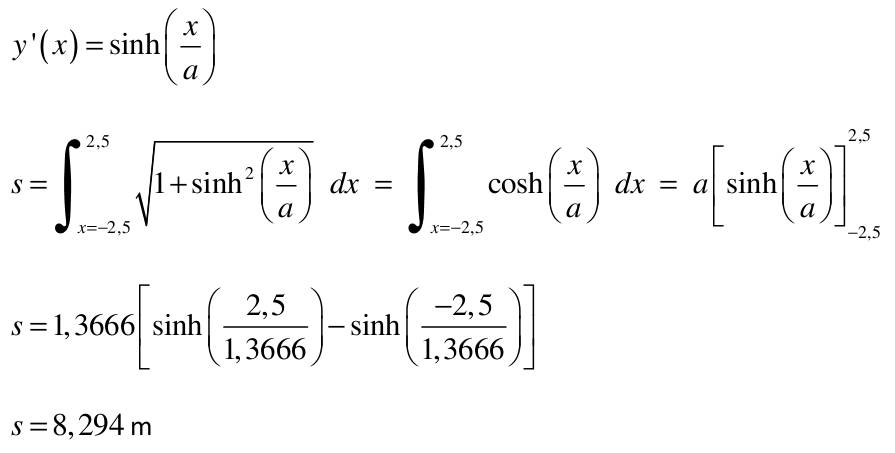 2) Ein Parabolspiegel wird durch die Rotation der Kurve y = k *x² um die y-Achse beschrieben. Wie groß ist seine Oberfläche für k = 1 / m = und 0 ≤ x ≤ 1 m (der Parabolspiegel hat also damit einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m).Vergleichen Sie die berechnete Oberfläche mit der einer Halbkugel vom Radius r = 1 m (Die Halbkugel hat auch einen Durchmesser von 2 m und eine Wölbungstiefe von 1 m). mit k = 1 und y`(x) = 2x 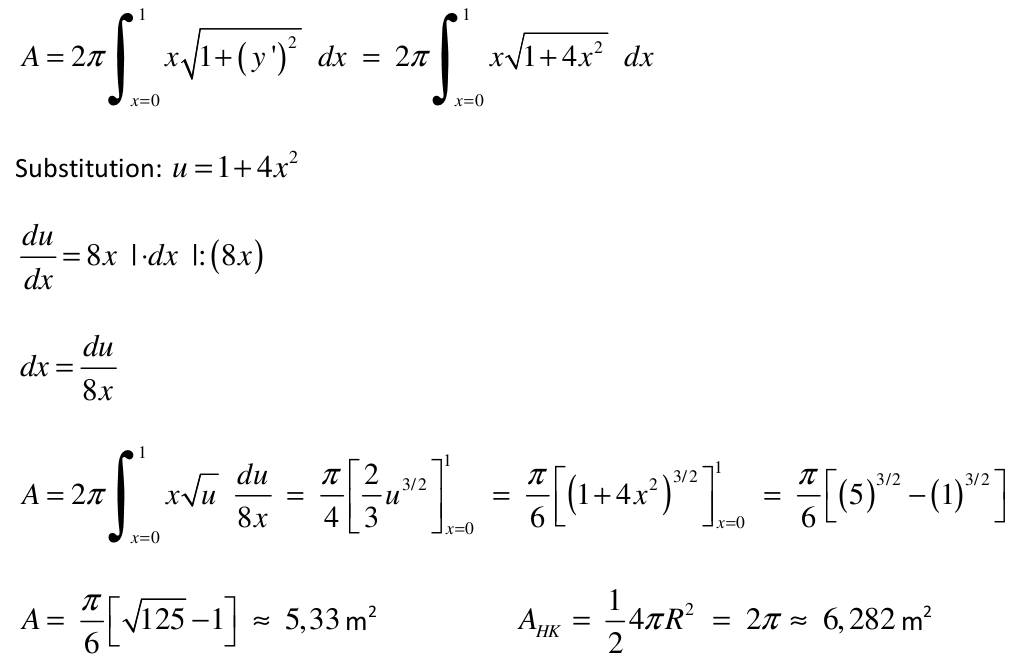 |
| PDF Dokument Lösungen Integralrechnung |
Diese Seite wurde noch nicht kommentiert.





