Version [58313]
Dies ist eine alte Version von TutoriumE3A1lsg erstellt von Jorina Lossau am 2015-08-25 16:02:51.
Tutorium Elektrotechnik 3
| File | Last modified | Size |
|---|---|---|
| Addition.jpg | 2023-10-06 18:37 | 22Kb |
| Addition2.jpg | 2023-10-06 18:37 | 22Kb |
| AdditionLoesung.jpg | 2023-10-06 18:37 | 4Kb |
| Division.jpg | 2023-10-06 18:37 | 36Kb |
| DivisionLoesung.jpg | 2023-10-06 18:37 | 7Kb |
| DivisionLoesungneu.jpg | 2023-10-06 18:37 | 8Kb |
| DivisionLoesungneu2.jpg | 2023-10-06 18:37 | 2Kb |
| Multiplikation.jpg | 2023-10-06 18:37 | 20Kb |
| MultiplikationLoesungneu.jpg | 2023-10-06 18:37 | 2Kb |
| PotenzierenLoesungneu2.jpg | 2023-10-06 18:37 | 2Kb |
| PotenzierenLoesungneu3.jpg | 2023-10-06 18:37 | 2Kb |
| Radizierenneu.jpg | 2023-10-06 18:37 | 3Kb |
| Radizierenneu2.jpg | 2023-10-06 18:37 | 3Kb |
| Radizierenneu3.jpg | 2023-10-06 18:37 | 2Kb |
| Subtraktion.jpg | 2023-10-06 18:37 | 18Kb |
| SubtraktionLoesung.jpg | 2023-10-06 18:37 | 4Kb |
| SubtraktionLoesung.png | 2023-10-06 18:37 | 3Kb |
| ZF1.jpg | 2023-10-06 18:37 | 12Kb |
| ZF2.jpg | 2023-10-06 18:37 | 21Kb |
| tutorium_get_3_teil_1_l�sungen.pdf | 2023-10-06 18:37 | 130Kb |
| tutorium_get_3_teil_1_loesungen.pdf | 2023-10-06 18:37 | 130Kb |
Teil 1: Wiederholung zu komplexen Zahlen - Lösungen
| Addition (arithmetische Form) - Aufgabe 1 |
|---|
z1+z2=a1+jb1+a2+jb2=(a1+a2)+j*(b1+b2) Gegeben sind folgende komplexe Zahlen: z1 = 3 + 4j z2 = 2 + 8j z3 = 4 - 7j z4 = 8 - 3j Bitte ermitteln Sie folgende Ausdrücke: z1+z2, z2+z3, z3+z4 a) arithmetisch b) graphisch Lösung: a) z1+z2 = 5+12j z2+z3=6+1j z3+z4=10-10j |
| Subtraktion (arithmetische Form) - Aufgabe 2 |
|---|
z1-z2=(a1+jb1)-(a2+jb2)=(a1-a2)+j*(b1-b2) Gegeben sind die komplexen Zahlen aus Aufgabe 1. Bitte ermitteln Sie folgende Ausdrücke: z1-z2, z2-z3, z3-z4 a)arithmetisch b)graphisch Lösung: z1-z2=1-4j z2-z3=-2+15j z3-z4=-4-4j |
| Multiplikation (arithmetische Form) - Aufgabe 3 |
|---|
z1*z2=(a1+jb1)*(a2+jb2)=a1a2+ja1b2+ja2b1+j²b1b2=a1a2-b1b2+j(a1b2+a2b1) Gegeben sind die komplexen Zahlen aus Aufgabe 1. Bitte ermitteln Sie arithmetisch folgende Ausdrücke: z1*z2,z2*z3,z3*z4 |
| Division (arithmetische Form) - Aufgabe 4 |
|---|
Wichtiger Hinweis: Um eine arithmetische Division durchzuführen müssen Zähler und Nenner mit dem konjugiert komplexen erweitert werden. 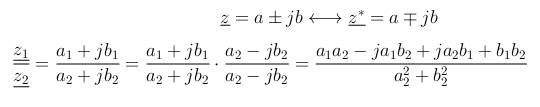 Gegeben sind die komplexen Zahlen aus Aufgabe 1. Bitte ermitteln Sie arithmetisch folgende Ausdrücke: z1/z2, z2/z3, z3/z4 |
| Multiplikation (Exponentialform) - Aufgabe 5 |
|---|
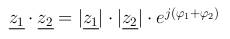 a) Bilden Sie die Exponentialform von den Ausdrücken aus Aufgabe 1. b) Multiplizieren Sie mit Hilfe der Exponentialschreibweise. c) Bilden Sie die arithmetische Form der Ergebnisse und geben Sie den Real- und den Imaginärteil an. |
| Division (Exponentialform) - Aufgabe 6 |
|---|
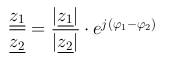 a) Bilden Sie die Exponentialform von den Ausdrücken aus Aufgabe 1. b) Dividieren Sie mit Hilfe der Exponentialschreibweise. c) Bilden Sie die arithmetische Form der Ergebnisse und geben Sie den Real- und den Imaginärteil an. |
| Potenzieren (Exponentialform) - Aufgabe 7 |
|---|
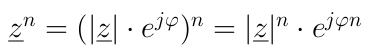 Wichtiger Hinweis: Beim Potenzieren kann es zu Winkeln kommen, die größer als 360 Grad sind. Solche Winkel signalisieren einen oder mehrere Umläufe des Zeigers in der komplexen Ebene. Um einen Winkel im Bereich zwischen 0 Grad und 360 Grad zu erhalten, muss mit einem Vielfachen von 360 Grad addiert bzw. subtrahiert werden. Berechnen Sie folgende Ausdrücke und geben Sie die Ergebnisse in arithmetischer, trigonometrischer und in Exponentialform an. 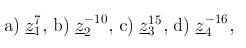 |
| Radizieren (Exponentialform) - Aufgabe 8 |
|---|
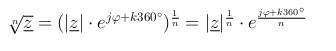 Wichtiger Hinweis: Durch da ziehen einer n- ten Wurzel, bekommt man immer n Lösungen. Im komplexen Zahlenbereich erhält man dadurch n Zeiger die alle um denselben Winkel voneinander entfernt sind. Die Lösungen lassen sich durch die Addition mit dem k-fachen von 360 im Argument ermitteln. Hierbei gilt. 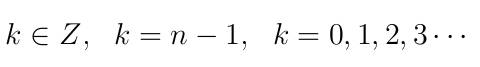 |
| PDF Dokument Lösungen Teil 1 |
Diese Seite wurde noch nicht kommentiert.





