Version [69194]
Dies ist eine alte Version von MikrooekonomieTut201415Aufgaben2 erstellt von Jorina Lossau am 2016-06-20 11:02:12.
Tutorium Mikroökonomie 2014/15
| File | Last modified | Size |
|---|---|---|
| Grafik1.jpg | 2023-10-06 18:37 | 7Kb |
| Grafik2.jpg | 2023-10-06 18:37 | 8Kb |
| Grafik3.jpg | 2023-10-06 18:37 | 11Kb |
| Grafik4.jpg | 2023-10-06 18:37 | 9Kb |
| Grafik5.jpg | 2023-10-06 18:37 | 8Kb |
| Grafik6.jpg | 2023-10-06 18:37 | 9Kb |
Klausur Sommersemester 2013
| Aufgabe 1: Haushaltstheorie (insgesamt 15 Punkte) a) Erläutern Sie, was es bedeutet, wenn die Einkomenselastizität für ein Gut größer als 1 ist. (3 P.) b) Können sich Indifferenzkurven schneiden? Erläutern Sie ihre Antwort. (3 P.) c) Was ist ein Giffen-Gut? Was ist ein normales Gut? (3 P.) d) Nehmen Sie an, dass die Güter x und y für Sie perfekte Komplemente sind. Welches der beiden folgenden Bündel ziehen Sie dann vor (i) eine Einheit von x und eine Einheit von y (ii) zwei Einheiten von x und eine Einheit von y? (3 P.) e) Nehmen Sie an, dass es zwei Güter gibt. Wie verändert sich die Budgetgerade, wenn die Preise beider Güter sich verdoppeln? (3 P.) Aufgabe 2: Haushaltstheorie (insgesamt 15 Punkte) a) Zeichnen Sie Grafiken mit Mengen von Gut 1 auf der horizontalen Achse und Mengen von Gut 2 auf der vertikalen Achse, um folgende Situationen zu illustrieren. Zeichnen Sie in jedem Fall zwei verschiedene Indifferenzkurven und kennzeichnen Sie die bevorzugte Richtung mit einem Pfeil. (i) Konsument A verabscheut beide Güter. (ii) Konsument B liebt Gut 1 und ist vollkommen indifferent bezüglich Gut 2. (4 P.) b) Wie verändert sich die Preiselastizität der Nachfrage in den verschiedenen Bereichen einer linearen Nachfragekurve? (4 P.) c) Eine Konsumentin, deren Präferenzen eine abnehmende Grenzrate der Substitution aufweisen, maximierte ihren Nutzen unter Berücksichtigung ihrer Budgetbedingung. Dann stieg der Preis des zweiten Gutes und der Preis des ersten Gutes fiel. Das Bündel, das sie ursprünglich im Optimum konsumierte, ist nach den Preisänderungen nicht länger erreichbar. Ist die Konsumentin nach der Preisänderung schlechter gestellt? Erläutern Sie ihre Antwort. (4 P.) d) Was ist eine inverse Nachfragefunktion? (3 P.) Aufgabe 3: Haushaltstheorie (insgesamt 15 Punkte) a)Ein Konsument habe die Nachfragefunktion x1=100-p1(x1 sei die Menge von Gut 1 und p1 der Preis des Gutes 1) Berechnen Sie die (direkte) Preiselastizität der Nachfrage.(4 P.) b) Ein Haushalt hat die Nutzenfunktion u=x1*x2. Dabei bezeichnen u den Nutzen, x1 die Menge von Gut 1, x2 die MEnge von Gut 2. Die Preise beider Güter betragen 10 Euro. Das Monatseinkommen beträgt 200 Euro. (b1) Berechnen Sie das optimale Bündel (4 P.) (b2) Wie hoch ist der Nutzen bei diesem Bündel (2 P.) (b3) Neben Sie an, bei Gut 1 handle es sich um Bücher. Der Haushalt bekommt nun folgendes Angebot von einem Buchclub: Wenn er eine Monatsgebühr von 100 Euro entrichtet, ist es möglich ein Buch für 2,50 Euro zu erhalten. Bestimmen Sie wiederum das optimale Güterbündel und das Nutzenniveau bei diesem Bündel. Wird sich der Haushalt für eine Mitgliedschaft entscheiden? (5 P.) Aufgabe 4: Haushaltstheorie (insgesamt 15 Punkte) a) Aggregieren Sie die beiden individuellen Nachfragefunktionen xA(p) = 810-0,5p und xB(p) = 90-0,1p der beiden Haushalte A und B zu einer Gesamtnachfragefunktion. Wie lautet die inverse Nachfrage (4 P.) b) Gegeben sei die Nutzenfunktion eines Individuums U(x1,x2)=x1^(1/2)* x2^(1/2). Die Budgetgerade sei durch p1x1+p2x2=m gegeben. Dabei bezeichnen m=1000 das Einkommen ,x1x2 die Mengen und p1-10, p2-20 die Preise der Güter 1 und 2. Wie lautet die neue Budgetgerade, falls eine Kopfsteuer T=80, eine Mengensteuer t1=0,5 auf Gut 1 eine Ausgabensteuer von 0,1 und eine Einkommensteuer mit dem proportionalen Steuersatz t=0,15 auf das Bruttoeinkommen erhoben werden? Wie hoch sind dann die Steuereinnahmen? (7 P.) c) Gegeben sei eine vollständige, reflexive, transitive, konvexe und monotone Präferenzrelation mit den davon abgeleiteten Relationen der strengen Präferenz und der Indifferenz. Ferner seien die Güterbündel x=(2, 5), y(5, 2) und z=(3, 4) gegeben. Aus der Sicht des betrachteten Individuums ist x genauso gut wie y und x ist genauso gut wie z. Ist dann das Güterbündel (4, 4) besser, schlechter oder gleich gut wie z? Begründen Sie Ihre Antwort. (4 P.) |
LösungAufgabe 1: Haushaltstheorie a) Wenn die Einkommenselastizität für ein Gut größer ist als 1, dann führt eine Einkommenssteigerung um 1% eine Nachfragesteigerung um mehr als 1% herbei. b) Aufgrund der Transitivität können sich Indifferenzkurven nicht schneiden 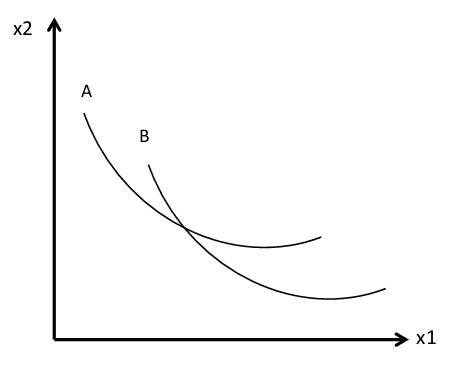 Wenn A~B und B~C dann müsste A~C aber da A und C offensichtlich nicht auf einer Indifferenzkurve liegen kann A nicht indifferent zu C sein. c) Bei Giffen Gut steigt mit steigendem Preis auch die Nachfrage. Bei einem normalen Gut geht die Nachfrage mit steigendem Preis zurück. d) Kann ohne eine Nutzenfunktion nicht bestimmt werden e) Wenn sich die Preise beider Güter verdoppeln erfolgt eine Parallelverschiebung in Richtung Koordinatenursprung. 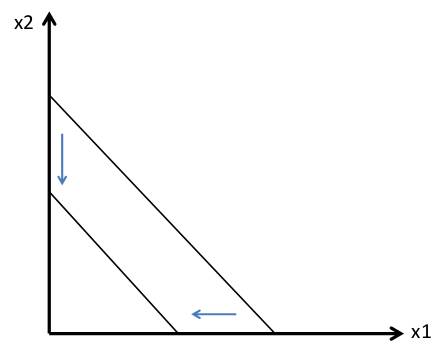 Aufgabe 2: Haushaltstheorie a) 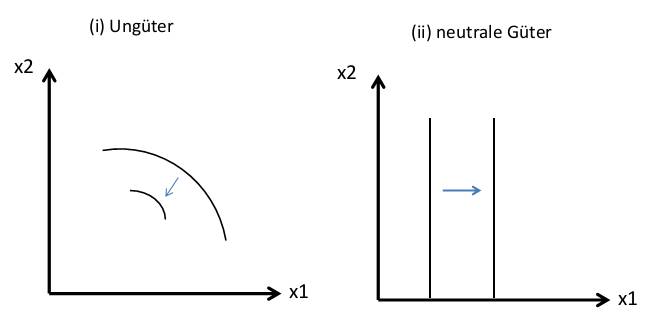 b) 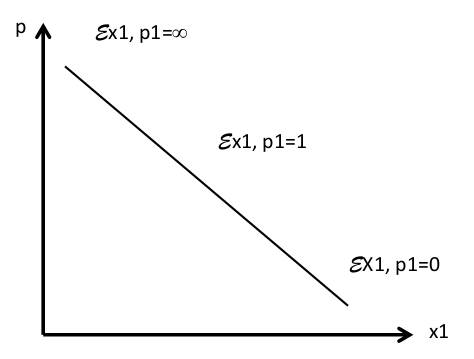 c) A = Ausgangsposition p2 nach oben und p1 nach unten A ist nicht länger erreichbar -> man kann keine Aussage darüber treffen, ob sich HH besser oder schlechter gestellt hat. 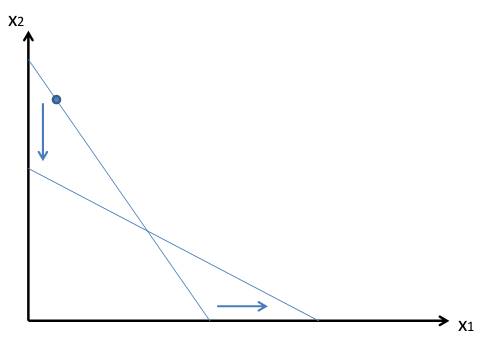 d) Die inverse Nachfragefunktion spiegelt den Preis als Funktion der Menge wieder ->p(x) Bsp.: Cobb-Douglas Funktion Nachfrage nach Gut 1 Direkte NF-Funktion: x1 = a* m/p1 Inverse NF-Funktion: p1 = a* m/x1 Aufgabe 3: Haushaltstheorie a) geg.: x1 = 100 - p1 ges.: εx1,p1 = (dx1/x1)/(dpi/p1) = ðx1p1/ðp1x1 1.) x1 nach p1 ableiten = -1 2.) -1* p1/x1 = -1* p1/(100-p1) = -p1/100-p1 b) geg.: U (x1, x2) = x1* x2 b1) streng monoton steigende Transformation ((U(x1,x2))^1/2 -> Cobb-Douglas NF U(x1,x2) = x1^0,5x2^0,5 x1* = a* m/p1 = 0,5 * 200/10 = 10 x2* = (1-a)* m/p2 = 0,5 *200/10 = 10 Das optimale Nutzungsbündel liegt bei (10,10) b2) U = 10*10 = 100 Der Nutzen an der Stelle (10,10) liegt bei 100 b3) m = 200 -100 Das Einkommen sinkt um 100 aufgrund der Mitgliedsgebühr x1* = 0,5* 100/2,5 = 20 x2* = 0,5* 100/10 = 5 U = 20* 0,5 Der neue Nutzen an der Stelle (20,5) liegt ebenfalls bei 100. Der HH ist somit indifferent d.h. eine Mitgliedschaft würde keinen zusätzlichen Nutzen erzeugen. Aufgabe 4: Haushaltstheorie a) xA(p) = 810 - 0,5p; xB(p) = 90 - 0,1p x = xA(p) + xB(p) -> x = 900-0,6p inverse NF: x umstellen nach p x = 900 - 0,6p -> x - 900 = -0,6 -> p = x-900/-0,6 -> p = 1500 - 1,67x b) Haushaltsoptimum: MRS = MOC -> MU1/MU2 = P1/P2 MU1/MU2 = (0,5*x1^-0,5*x2^0,5)/(x1^0,5*0,5*x2^-0,5) = x2/x1 -> x2/x1 = 10/20 -> x2 = 0,5* x1 (1-t)* m - T = t1* x1 + (1+r)* p1x1 + (1+r) * p2x2 (1-0,15)*1000 - 80 = 0,5* x1 + 1,1* 10x1 + 1,1* 20x2 770 = 11,5x1 + 1,1* 20* 0,5*x1 770 = 22,5x1 -> x1* = 34,22 x2 = 0,5*x1 -> x2* = 17,11 Steuereinnahmen = 150 + 80 + 0,5* x1 + 0,1* (10x1* + 20x2*) = 315,56 c) Das Güterbündel (4/4) liegt außerhalb der Budgetgerade. Aufgrund von Monotonie ("mehr ist besser") stellt sich der HH besser. 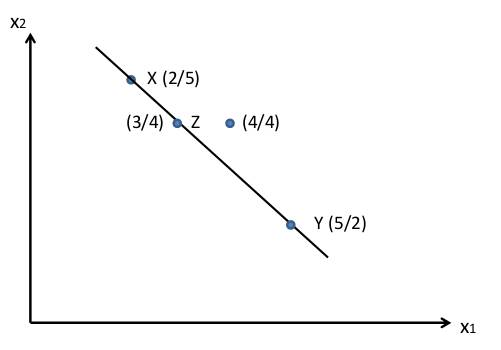 |
Diese Seite wurde noch nicht kommentiert.





