Version [62805]
Dies ist eine alte Version von MatheGKL4 erstellt von Jorina Lossau am 2015-12-08 17:33:23.
Tutorium Mathematischer Grundkurs
Gaußsches Eliminierungsverfahren - Lösungen
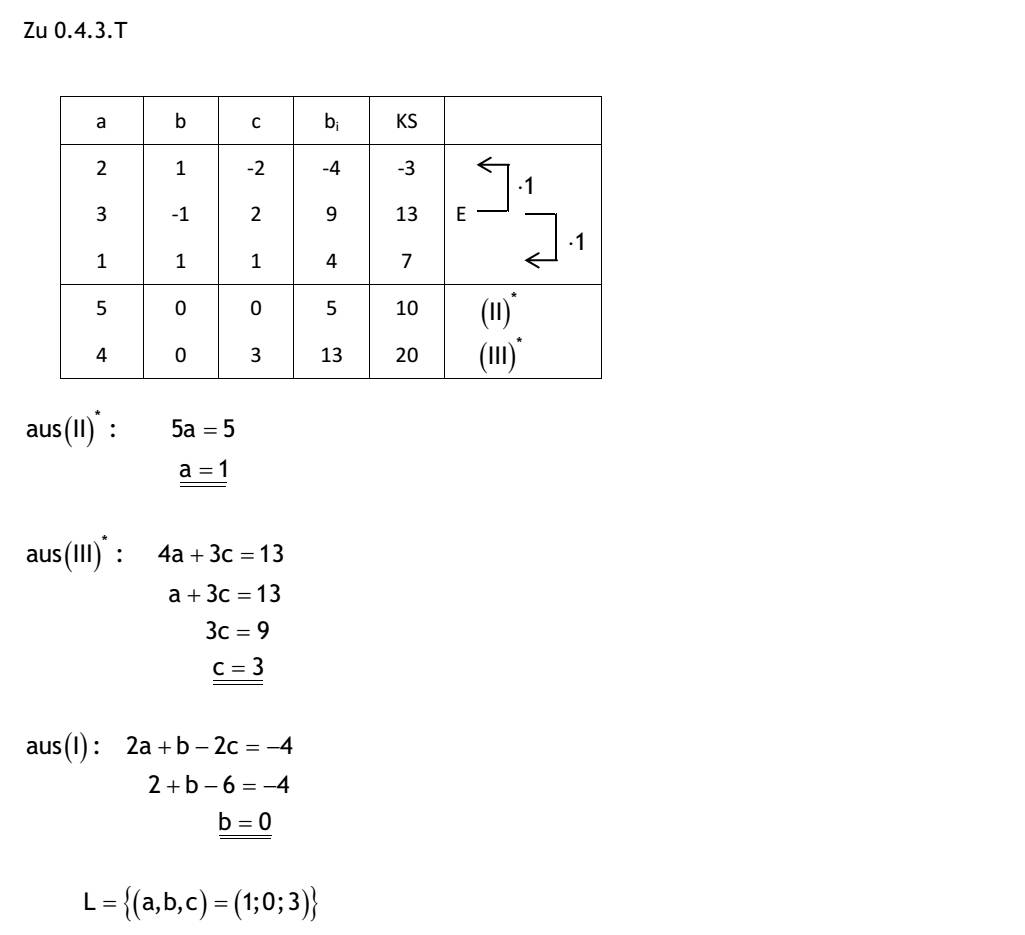
| 0.4.1.T Lösen Sie mit dem Gauß'schen Eliminierungsverfahren (ausführliche Schreibweise) 3x + 2y + 4z = 9 (I) -x + y = -5 (II) 2x - 2z = 4 (III) 8x + 6y + 4z = 16 (IV) 0.4.2.T Lösen Sie mit dem Gauß'schen Eliminierungsverfahren (verkürzte Schreibweise) 2a + b - 2c = -4 (I) 3a - b + 2c = 9 (II) 4a - 3b + 6c = 22 (III) 0.4.3.T Lösen Sie mit dem Gauß'schen Verfahren in der Koeffizientenschreibform 2a + b - 2c = -4 (I) 3a - b + 2c = 9 (II) a + b + c = 4 (III) Lösung: zu 0.4.1.T 3x + 2y + 4z = 9 (I) -x + y = -5 (II) 2x - 2z = 4 (III) 8x + 6y + 4z = 16 (IV) -x + y = -5 3* (II) + (I) 5y + 4z = -6 (II) 2* (II) + (III) 2y - 2z =-6 (III) 8* (II) + (IV) 14y + 4z = -24 -x + y = -5 2y - 2z = -6 2* (III) + (II) 9y = -18 -> y= -2 aus (II): x = y+5 = -2 + 5 -> x =3 aus (III): z = (2x-4)/2 = (6-4)/2 -> z = 1 L = {3;-2;1} |
| PDF Dokument Lösungen Gaußsches Eliminierungsverfahren |
Diese Seite wurde noch nicht kommentiert.





