Der Satz von Bayes
Der Satz von Bayes ist einer der wichtigsten Sätze in der Wahrscheinlichkeit.
1. Die Formel:
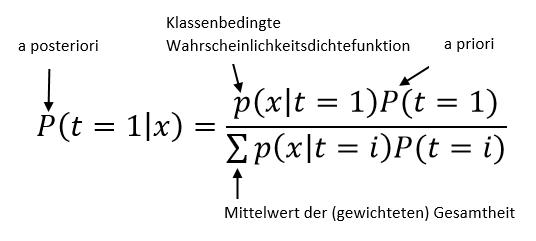
Es ist ein Satz der Bedingten Wahrscheinlichkeit, beschreibt also wie Wahrscheinlich ein Ereignis (t=1) ist, unter der Bedingung dass x eingetreten ist.
2. Rechenbeispiele:
a. Die Vogelgrippe:
Die Vogelgrippe ist eine seltene Krankheit, die Nutzvögel wie zum Beispiel Hühner befallen kann.
Sie ist so selten, dass von 10.000 Hühnern nur zwei krank ist.
Es wurde ein Test entwickelt, der die Krankheit bei kranken Hühnern mit 99.9% erkennt.
Allerdings schlägt er zu 5% auch bei gesunden Hühnern an.
Wie Wahrscheinlich ist es nun, dass ein Huhn krank ist, wenn der Test positiv ausfällt?
t=1 := "Das Huhn ist krank."
t=2 := "Das Huhn ist gesund."
x := "Der Test ist positiv."
Die a priori Wahrscheinlichkeit dafür, dass ein Huhl krank ist, ist
formel
P(t=1) =formel
formel
2 \over 10.000formel
formel
= 0,0002formel
Die klassenbedingte Wahrscheinlichkeitsdichte, beschreibt wie gut der Test kranke Hühner erkennt:
Die Wahrscheinlichkeit dafür, dass der Test positiv ist unter der Bedingung, dass das getestete Huhn krank ist, ist
formel
p(x|t=1) =formel
99,9%formel
= 0,999formel
Der Mittelwert der Gesamtheit der positiv ausfallenden Test, ist die totale Wahrscheinlichkeit, dass ein Test positiv ausfällt.
(Nach dem Satz der totalen Wahrscheinlichkeit, ist
formel
p(x) =formel
)formel
\sum p(x|t=i)P(t=i) = p(x|t=1)P(t=1) + p(x|t=2)P(t=2) = 0,999*0,0002 + 0,05*0,9999formel
Damit ergibt sich für
formel
P(t=1|x)=formel
formel
p(x|t=1)P(t=1) \over \sum p(x|t=i)P(t=i)formel
=formel
p(x|t=1)P(t=1) \over p(x|t=1)P(t=1) + p(x|t=2)P(t=2)formel
=formel
0,999*0,0002 \over 0,999*0,0002 + 0,05*0,9999formel
formel
= 0,00398formel
Das bedeutet, dass von 250 positiv getesteten Hühnern nur ein einziges wirklich krank sind.
Der Satz von Bayes erfragt nicht, ob ein Test richtig funktionier, sondern ob er a posteriori richtig erkannt hat.
Die Wahrscheinlichkeit ein krankes Huhn zu erkennen liegt bei 99.9%, die Wahrscheinlichkeit das ein Huhn wirklich krank ist nur bei 0,004.
b. Buchstabenerkennung
Ein Algorithmus soll eingescannte deutsche Texte erkennen. Der Algorithmus hat kleine Probleme mit u und v, hier irrt er sich zu 1%.
Die Wahrscheinlichkeit für ein u in einem deutschen Text ist 4,3% (P(t=1)=0,043). V's sind seltener und tauchen nur mit 0.67% auf (P(t=2)=0,0067).
Wie Wahrscheinlichkeit ist ein als v erkannter Buchstabe wirklich ein v? (P(t=2|x) (a posteriori)?)
Wahrscheinlichkeit für ein u: P(t=1)=0,043
Wahrscheinlichkeit für ein v: P(t=2)=0,0067 (a priori)
Test erkennt v als v: p(x|t=2) = 0,99
Test erkennt u als v: p(x|t=1) = 0,01
Test erkennt ein v:
formel
\sum p(x|t=i)P(t=i) = p(x|t=1)P(t=1) + p(x|t=2)P(t=2) = 0,043*0,01 + 0,0067*0,99formel
(Satz der totalen Wahrscheinlichkeit)Damit ergibt sich:
formel
P(t=2|x) =formel
formel
p(x|t=2)P(t=2) \over \sum p(x|t=i)P(t=i)formel
=formel
p(x|t=2)P(t=2) \over p(x|t=1)P(t=1) + p(x|t=2)P(t=2)formel
=formel
0,0067*0,99 \over 0,043*0,01 + 0,0067*0,99formel
formel
= 0,939formel
Ein vom Test als v erkannter Buchstabe ist also zu 93,9% wirklich ein v, obwohl sich der Test nur in 1% der Fälle irrt.
In einem englischen Text tritt ein u zu 2,8% und ein v zu 0,98% ein. Die Wahrscheinlichkeit, dass ein erkanntes v wirklich ein v ist, liegt in englischen Texten immerhin schon bei 97%.
3. abstraktes Beispiel
Wir messen die Größe der Menschen.
formel
\frac 2 3formel
aller gemessenen Menschen sind männlich. (->formel
p(t=1)= \frac 2 3formel
). Wie erhalten folgendes Histogramm: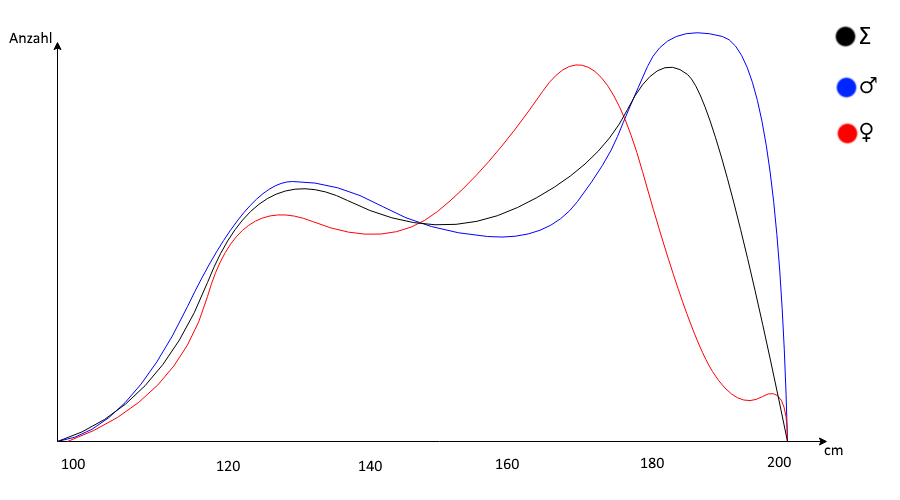
Mit Hilfe von Bayes können wir jetzte die Wahrscheinlichkeitsdichtefunktion berechnen und erhalten:
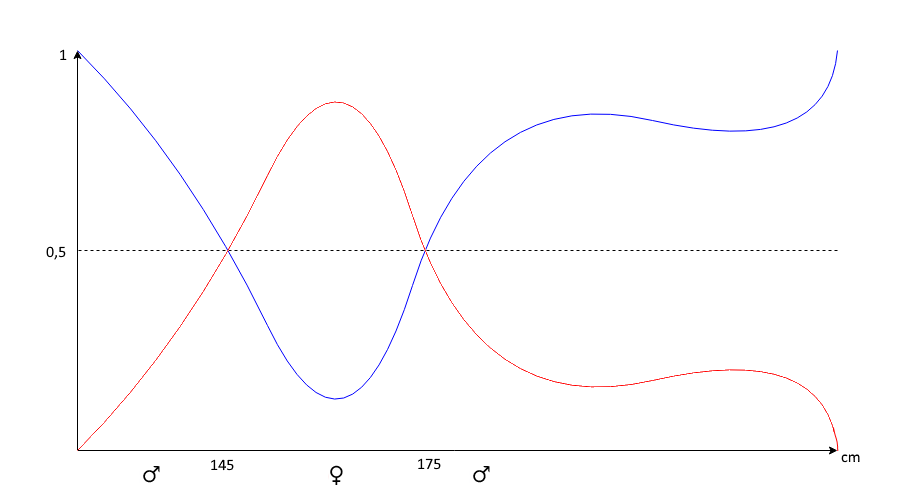
Mit Hilfe dieser Dichte kann nun auf einen Blick die Wahrscheinlichere Klasse (♂ oder ♀) abgelesen werden.
(Bayes ist ein optimaler Klassifikator.)
Quelle:
Stochastik - Strucktur im Zufall von Matthias Löwe, Holger Knöpfel (2. Auflage, 9783486706765)
https://de.wikipedia.org/wiki/Buchstabenhäufigkeit
Diese Seite wurde noch nicht kommentiert.





